Question

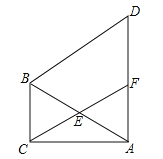
【题目】如图是一座人行天桥的引桥部分的示意图，梯面AD、BE相互平行，且与地面成37°的夹角，DE是一段水平歇台，离地面高度3米．已知天桥高度BC为4.8米，引桥水平跨度AC为8米，求梯面AD、BE及歇台DE的长．（参考数据：，结果保留两位小数）

Answer 1

【答案】5.00；3.00；1.60

【解析】

过分别点D、E作DF⊥AC，EG⊥BC，垂足分别为点F、G．解直角三角形ADF求得AD，AF，再解直角三角形BEG，得出BE、BG的长即可得出DE的长．

解：过分别点D、E作DF⊥AC，EG⊥BC，垂足分别为点F、G．

在Rt中，，DF=3

∴，

即，

∴，

∵AD∥BE

∴

在Rt中，，BG=1.8

∴，即，

∴，

∴DE=AC-EG-AF=8-2.4-4=1.60