题目内容
| a1 |
| |a1| |
| a2 |
| |a2| |
| a3 |
| |a3| |
| a9 |
| |a9| |
考点:绝对值
专题:分类讨论
分析:当a>0,
=1,当a<时
=-1,按此分类讨论即可.
| a |
| |a| |
| a |
| |a| |
解答:解:当a>0,
=1,当a<时
=-1,按此分类讨论,
当a1、a2、a3、…、a9均为正数时,
+
+
+…+
=9,
当a1、a2、a3、…、a9有八个为正数,一个为负数时,
+
+
+…+
=8-1=7,
当a1、a2、a3、…、a9有七个为正数,两个为负数时,
+
+
+…+
=7-2=5,
当a1、a2、a3、…、a9有六个为正数,三个为负数时,
+
+
+…+
=6-3=3,
当a1、a2、a3、…、a9有五个为正数,四个为负数时,
+
+
+…+
=5-4=1,
当a1、a2、a3、…、a9有四个为正数,五个为负数时,
+
+
+…+
=4-5=-1,
当a1、a2、a3、…、a9有三个为正数,六个为负数时,
+
+
+…+
=3-6=-3,
当a1、a2、a3、…、a9有两个为正数,七个为负数时,
+
+
+…+
=2-7=-5,
当a1、a2、a3、…、a9有一个为正数,八个为负数时,
+
+
+…+
=1-8=-7,
当a1、a2、a3、…、a9均为负数时,
+
+
+…+
=-9,
所以共有10个值,
故答案为:10.
| a |
| |a| |
| a |
| |a| |
当a1、a2、a3、…、a9均为正数时,
| a1 |
| |a1| |
| a2 |
| |a2| |
| a3 |
| |a3| |
| a9 |
| |a9| |
当a1、a2、a3、…、a9有八个为正数,一个为负数时,
| a1 |
| |a1| |
| a2 |
| |a2| |
| a3 |
| |a3| |
| a9 |
| |a9| |
当a1、a2、a3、…、a9有七个为正数,两个为负数时,
| a1 |
| |a1| |
| a2 |
| |a2| |
| a3 |
| |a3| |
| a9 |
| |a9| |
当a1、a2、a3、…、a9有六个为正数,三个为负数时,
| a1 |
| |a1| |
| a2 |
| |a2| |
| a3 |
| |a3| |
| a9 |
| |a9| |
当a1、a2、a3、…、a9有五个为正数,四个为负数时,
| a1 |
| |a1| |
| a2 |
| |a2| |
| a3 |
| |a3| |
| a9 |
| |a9| |
当a1、a2、a3、…、a9有四个为正数,五个为负数时,
| a1 |
| |a1| |
| a2 |
| |a2| |
| a3 |
| |a3| |
| a9 |
| |a9| |
当a1、a2、a3、…、a9有三个为正数,六个为负数时,
| a1 |
| |a1| |
| a2 |
| |a2| |
| a3 |
| |a3| |
| a9 |
| |a9| |
当a1、a2、a3、…、a9有两个为正数,七个为负数时,
| a1 |
| |a1| |
| a2 |
| |a2| |
| a3 |
| |a3| |
| a9 |
| |a9| |
当a1、a2、a3、…、a9有一个为正数,八个为负数时,
| a1 |
| |a1| |
| a2 |
| |a2| |
| a3 |
| |a3| |
| a9 |
| |a9| |
当a1、a2、a3、…、a9均为负数时,
| a1 |
| |a1| |
| a2 |
| |a2| |
| a3 |
| |a3| |
| a9 |
| |a9| |
所以共有10个值,
故答案为:10.
点评:此题主要考查分类讨论能力,解题的关键是充分利用好
=±1这一结论,注意分类的准确.
| a |
| |a| |

练习册系列答案
相关题目
顺次连接四边形四边中点所组成的四边形是矩形,则原四边形为( )
| A、平行四边形 |
| B、对角线垂直的四边形 |
| C、对角线相等的四边形 |
| D、直角梯形 |
 如图,正方形A1B1B2C1,A2B2B3C2,A3B3B4C3,…,AnBnBn+1Cn,按如图所示放置,使点A1、A2、A3、A4、…、An在射线OA上,点B1、B2、B3、B4、…、Bn在射线OB上.若∠AOB=45°,OB1=1,图中阴影部分三角形的面积由小到大依次记作S1,S2,S3,…,Sn,则Sn=
如图,正方形A1B1B2C1,A2B2B3C2,A3B3B4C3,…,AnBnBn+1Cn,按如图所示放置,使点A1、A2、A3、A4、…、An在射线OA上,点B1、B2、B3、B4、…、Bn在射线OB上.若∠AOB=45°,OB1=1,图中阴影部分三角形的面积由小到大依次记作S1,S2,S3,…,Sn,则Sn= 如图,正方形ABCD的边长为8,E、F分别为BC、CD边上的点,且tan∠EAF=
如图,正方形ABCD的边长为8,E、F分别为BC、CD边上的点,且tan∠EAF=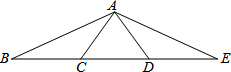 如图,若∠BAC=37°,且AC=BC=AD=DE,则∠BAE=
如图,若∠BAC=37°,且AC=BC=AD=DE,则∠BAE=