题目内容
阅读以下短文,然后解决下列问题:
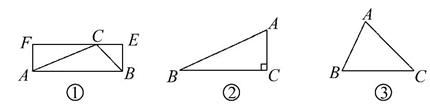
如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”.如图①所示,矩形ABEF即为△ABC的“友好矩形”.显然,当△ABC是钝角三角形时,其“友好矩形”只有一个.
(1)仿照以上叙述,说明什么是一个三角形的“友好平行四边形”.
(2)如图②,若△ABC为直角三角形,且∠C=90°,在图②中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小.
(3)若△ABC是锐角三角形,且BC>AC>AB,在图③中画出△ABC的所有“友好矩形”,指出其中周长最小的矩形并加以证明.
(1)如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角 形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四
形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四 边形”.
边形”.
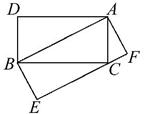 (2)此时共有2个“友好矩形”,如图,矩形BCAD,矩形ABEF.
(2)此时共有2个“友好矩形”,如图,矩形BCAD,矩形ABEF.
易知,矩形BCAD,矩形ABEF的面积都等于△ABC面积的2倍,
∴△ABC的“友好矩形”的面积相等.
(3)此时共有3个“友好矩形”,如 图中矩形BCDE,矩形CAFG及矩形ABHK,其中矩形ABHK的周长最小.
图中矩形BCDE,矩形CAFG及矩形ABHK,其中矩形ABHK的周长最小.

证明如下:易知,这三个矩形的面积相等,令 其为S.设矩形BCDE,矩形CAFG及矩形ABHK的周长分别为L1,L2,L3,△ABC的边长BC=a,CA=b,AB=c,则L1=
其为S.设矩形BCDE,矩形CAFG及矩形ABHK的周长分别为L1,L2,L3,△ABC的边长BC=a,CA=b,AB=c,则L1=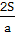 +2a,L2=
+2a,L2=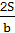 +2b,L3=
+2b,L3=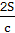 +2c.
+2c.
∴L1-L2=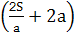 -
-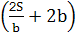 =2(a-b)×
=2(a-b)× ,而ab>S,a>b,∴L1- L2>0,即L1> L2.
,而ab>S,a>b,∴L1- L2>0,即L1> L2.
同理可得,L2> L3,
∴L3最小,即矩形ABHK的周长最小.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案声音在空气中传播的速度y( m/s)(简称音速)与气温x(℃)之间的关系
m/s)(简称音速)与气温x(℃)之间的关系 如下:
如下:
| 气温(x/℃) | 0 | 5 | 10 | 15 | 20 |
| 音速 | 331 | 334 | 337 | 340 | 343 |
从表中可知 音速y随温
音速y随温 度x的升高而加快.运动会当天
度x的升高而加快.运动会当天 的气温为20℃,某人看到发令枪的烟0.2s后,听到了枪声,则由此可知,这个人距发令地点 m.
的气温为20℃,某人看到发令枪的烟0.2s后,听到了枪声,则由此可知,这个人距发令地点 m.
 =
= ,其中变量是( )
,其中变量是( )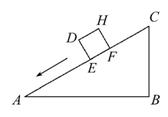

 ,BC,CD的中点.若
,BC,CD的中点.若 AC=8,BD=6,则四边形EFGH的面积为 .
AC=8,BD=6,则四边形EFGH的面积为 .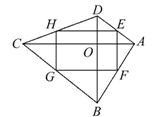
 AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
 正确,乙错误 B.乙正确,甲错误
正确,乙错误 B.乙正确,甲错误 x的共同特点是( )
x的共同特点是( )