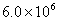题目内容
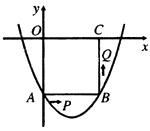
如图在平面直角坐标系xoy中,正方形OABC的边长为2厘米,点A、C分别在y轴的负半轴和x轴的正半轴上.抛物线y=ax2+bx+c经过点A ,B和点 D(4, 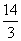 )
)
(1)求抛物线的解析式;
(2)如果点P由点A开始沿AB边以2厘米/秒的速度向点B移动,同时点Q由B点开始沿BC边以1厘米/秒的速度向点C移动.若P、Q中有一点到达终点,则另一点也停止运动,设P、Q两点移动的时间为t秒,S=PQ2(厘米2)
写出S与t之间的函数关系式,并写出t的取值范围,当t为何值时,S最小;
(3)当s取最小值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出点R的坐标;如果不存在,请说明理由.
(4)在抛物线的对称轴上求出点M,使得M到D,A距离之差最大?写出点M的坐标.
(1)
(2)S=PQ2=5t2-8t+4(0≤t≤1),当 时,S最小
时,S最小
(3)若以BQ为一条对角线,四边形PBRQ为平行四边形,
 时,
时, ,在
,在 中,
中,
当 时,
时, .
.
∴R在抛物线上.
若PB为对角线,当 时,
时,
在 中,当
中,当 时,
时, ,
,
∴ 不在抛物线上,
不在抛物线上,
综上可知,抛物线上存在
使以P、B、Q、R为顶点的四边形是平行四边形.
(4)M(1, )
)

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 时,请计算输出的结果
时,请计算输出的结果 的值
的值

 为格点三角形(即三角形的顶点都在格点上).
为格点三角形(即三角形的顶点都在格点上).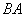 方向平移后,点
方向平移后,点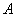 移到点
移到点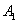 ,在网格中画出平移后得到的
,在网格中画出平移后得到的 ;
;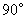 ,在网格中画出旋转后的
,在网格中画出旋转后的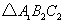 ;
; 经过(1)、(2)变换的路径总长.
经过(1)、(2)变换的路径总长.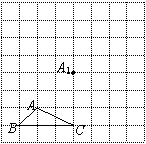
 . (B)
. (B) . (C)
. (C) . (D)
. (D) .[
.[ ,圆心距O1O2=4,则两圆的位置关系是 .
,圆心距O1O2=4,则两圆的位置关系是 .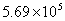 B.
B.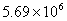 C.
C. D.
D.