题目内容
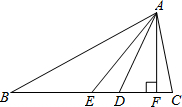 如图,在△ABC中,AE是中线,AD是角平分线,AF是高,∠B=30°,∠C=80°,BE=2,AF=3,填空:
如图,在△ABC中,AE是中线,AD是角平分线,AF是高,∠B=30°,∠C=80°,BE=2,AF=3,填空:(1)AB=
(2)∠BAD=
(3)∠DAF=
(4)S△AEC=
考点:三角形的角平分线、中线和高
专题:
分析:(1)根据30°角所对的直角边等于斜边的一半可得AB=2AF=6;
(2)先由三角形内角和定理求出∠BAC=70°,再根据角平分线定义得到∠BAD=
∠BAC=35°;
(3)先由三角形内角和定理求出∠FAC=10°,再根据∠DAF=∠DAC-∠FAC即可求解;
(4)先由三角形中线的定义得出EC=BE=2,再根据S△AEC=
EC•AF即可求解.
(2)先由三角形内角和定理求出∠BAC=70°,再根据角平分线定义得到∠BAD=
| 1 |
| 2 |
(3)先由三角形内角和定理求出∠FAC=10°,再根据∠DAF=∠DAC-∠FAC即可求解;
(4)先由三角形中线的定义得出EC=BE=2,再根据S△AEC=
| 1 |
| 2 |
解答:解:(1)∵在△ABF中,AF是高,∠B=30°,AF=3,
∴AB=2AF=6;
(2)∵在△ABC中,∠B=30°,∠C=80°,
∴∠BAC=70°,
∵AD是角平分线,
∴∠BAD=
∠BAC=35°;
(3)∵在△AFC中,AF是高,∠C=80°,
∴∠FAC=10°,
∴∠DAF=∠DAC-∠FAC=35°-10°=25°;
(4)∵在△ABC中,AE是中线,
∴EC=BE=2,
∴S△AEC=
EC•AF=
×2×3=3.
故答案为6;35°;25°;3.
∴AB=2AF=6;
(2)∵在△ABC中,∠B=30°,∠C=80°,
∴∠BAC=70°,
∵AD是角平分线,
∴∠BAD=
| 1 |
| 2 |
(3)∵在△AFC中,AF是高,∠C=80°,
∴∠FAC=10°,
∴∠DAF=∠DAC-∠FAC=35°-10°=25°;
(4)∵在△ABC中,AE是中线,
∴EC=BE=2,
∴S△AEC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为6;35°;25°;3.
点评:本题考查了三角形的角平分线、中线和高,从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高;三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线;三角形一边的中点与此边所对顶点的连线叫做三角形的中线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
若x2-x-n=(x-m)(x-3),则mn=( )
| A、6 | B、4 | C、12 | D、-12 |
已知分式
与分式
的值相等,则x=( )
| x-2 |
| x-3 |
| x+1 |
| x-1 |
| A、1 | B、2 | C、3 | D、5 |
 如图D、A、C、B为⊙O上的点,DC=AB,则AD与BC的大小关系是( )
如图D、A、C、B为⊙O上的点,DC=AB,则AD与BC的大小关系是( )| A、AD>BC | B、AD=BC |
| C、AD<BC | D、不能确定 |
 如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD=100°,则∠DCE的大小是( )
如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD=100°,则∠DCE的大小是( )| A、115° | B、105° |
| C、100° | D、95° |
 如图,?ABCD的两条对角线线交于O,且
如图,?ABCD的两条对角线线交于O,且