题目内容
5.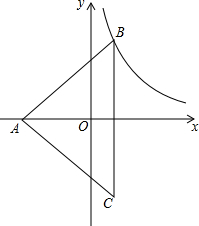 如图,等腰三角形ABC的外心与原点重合,AB=AC=10,BC=12,顶点A在x轴负半轴,顶点B在反比例函数y=$\frac{k}{x}$位于第一象限的图象上,则k的值为$\frac{21}{2}$.
如图,等腰三角形ABC的外心与原点重合,AB=AC=10,BC=12,顶点A在x轴负半轴,顶点B在反比例函数y=$\frac{k}{x}$位于第一象限的图象上,则k的值为$\frac{21}{2}$.
分析 设BC与x轴相交于点D,连接OB,先根据AB=AC=10,BC=12,点O是△ABC的外心可知AD是BC的垂直平分线,OB=OA,再根据勾股定理求出AD的长,设OD=x,则OA=OB=8-x,在Rt△BOD中根据勾股定理求出x的值,故可得出B点坐标,代入反比例函数的解析式即可得出结论.
解答 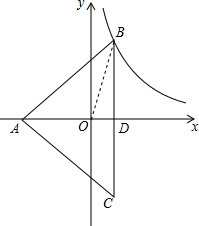 解:设BC与x轴相交于点D,连接OB,
解:设BC与x轴相交于点D,连接OB,
∵AB=AC=10,BC=12,点O是△ABC的外心,
∴AD是BC的垂直平分线,OB=OA,
∴BD=$\frac{1}{2}$BC=6,
∴AD=$\sqrt{{AB}^{2}-{BD}^{2}}$=$\sqrt{{10}^{2}-{6}^{2}}$=8.
设OD=x,则OA=OB=8-x,
在Rt△BOD中,OB2=OD2+BD2,即(8-x)2=x2+62,解得x=$\frac{7}{4}$,
∴B($\frac{7}{4}$,6),
∴k=$\frac{7}{4}$×6=$\frac{21}{2}$.
故答案为:$\frac{21}{2}$.
点评 本题考查的是三角形的外接圆与外心,熟知三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心是解答此题的关键.

练习册系列答案
相关题目
13.某项工程的投资为12000元,这个数用科学记数法表示为( )
| A. | 12×104元 | B. | 1.2×104元 | C. | 1.2×105元 | D. | 1.2×106元 |
10.下列各数:$\frac{1}{3}$,π,$\root{3}{8}$,0,$\sqrt{3}$,其中无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.估计$\sqrt{5}$+1在( )
| A. | 0~1之间 | B. | 1~2之间 | C. | 2~3之间 | D. | 3~4之间 |
14. 如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠ACB相等的角有( )
如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠ACB相等的角有( )
 如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠ACB相等的角有( )
如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠ACB相等的角有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
 如图,在⊙O中,AB为⊙O的直径,C,D为⊙O的两点,若∠ADC=56°,则∠BAC=34°.
如图,在⊙O中,AB为⊙O的直径,C,D为⊙O的两点,若∠ADC=56°,则∠BAC=34°. 一个全透明的正方体上面嵌有一根黑色的金属丝,如图所示,金属丝在俯视图中的形状是( )
一个全透明的正方体上面嵌有一根黑色的金属丝,如图所示,金属丝在俯视图中的形状是( )



 如图,已知D、E为半圆$\widehat{AB}$的三等分点,若AB=2,则图中阴影部分的面积为$\frac{1}{6}$π.
如图,已知D、E为半圆$\widehat{AB}$的三等分点,若AB=2,则图中阴影部分的面积为$\frac{1}{6}$π.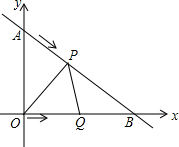 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.