题目内容
20. 如图,已知D、E为半圆$\widehat{AB}$的三等分点,若AB=2,则图中阴影部分的面积为$\frac{1}{6}$π.
如图,已知D、E为半圆$\widehat{AB}$的三等分点,若AB=2,则图中阴影部分的面积为$\frac{1}{6}$π.
分析 连接OC、OD,利用同底等高的三角形面积相等可知阴影部分的面积等于扇形OCD的面积,然后计算扇形面积就可.
解答  解:连接OD、OE.
解:连接OD、OE.
∵△DOE和△COA等底等高,
∴S△DOE=S△AOC.
∵点C,D为半圆的三等分点,
∴∠DOE=180°÷3=60°,
∴阴影部分的面积=S扇形DOE=$\frac{60π×{1}^{2}}{360}$=$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 此题主要考查了扇形面积求法,利用已知得出理解阴影部分的面积等于扇形OCD的面积是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列事件属于不可能事件的是( )
| A. | 两点确定一条直线 | |
| B. | 两点之间线段最短 | |
| C. | 在同一平面内,垂直于同一条直线的两条直线互相垂直 | |
| D. | 在同一平面内,平行于同一条直线的两条直线互相平行 |
11.下列图形中,既是轴对称又是中心对称的图形是( )
| A. | 直角三角形 | B. | 正五边形 | C. | 正六边形 | D. | 等腰梯形 |
12. 如图为某羽毛球场馆的两种计费方案说明.若王老板和朋友们打算在此羽毛球场馆里连续打球6小时,经服务生试算后,告知他们选择包场计费方案会比人数计费方案便宜,则他们至少有多少人参与包场?( )
如图为某羽毛球场馆的两种计费方案说明.若王老板和朋友们打算在此羽毛球场馆里连续打球6小时,经服务生试算后,告知他们选择包场计费方案会比人数计费方案便宜,则他们至少有多少人参与包场?( )
 如图为某羽毛球场馆的两种计费方案说明.若王老板和朋友们打算在此羽毛球场馆里连续打球6小时,经服务生试算后,告知他们选择包场计费方案会比人数计费方案便宜,则他们至少有多少人参与包场?( )
如图为某羽毛球场馆的两种计费方案说明.若王老板和朋友们打算在此羽毛球场馆里连续打球6小时,经服务生试算后,告知他们选择包场计费方案会比人数计费方案便宜,则他们至少有多少人参与包场?( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
9.下列选项不正确的是( )
| A. | 两直线平行,同位角相等 | |
| B. | 对顶角相等 | |
| C. | ∵∠1=∠2,∠2=∠3,∴∠1=∠3 | |
| D. | 两条直线被第三条直线所截,同旁内角互补 |
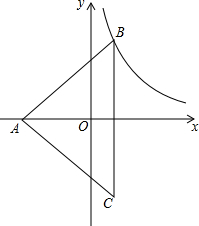 如图,等腰三角形ABC的外心与原点重合,AB=AC=10,BC=12,顶点A在x轴负半轴,顶点B在反比例函数y=$\frac{k}{x}$位于第一象限的图象上,则k的值为$\frac{21}{2}$.
如图,等腰三角形ABC的外心与原点重合,AB=AC=10,BC=12,顶点A在x轴负半轴,顶点B在反比例函数y=$\frac{k}{x}$位于第一象限的图象上,则k的值为$\frac{21}{2}$.