题目内容
观察下列等式:
=1-
;
=
-
;
=
-
;
=
-
;…,
(1)按以上规律,则
= ;
(2)求
+
+
+…+
的值;
(3)探究并解方程:
+
+
=
.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
(1)按以上规律,则
| 1 |
| n(n+1) |
(2)求
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
(3)探究并解方程:
| 1 |
| x(x+2) |
| 1 |
| (x+2)(x+4) |
| 1 |
| (x+4)(x+6) |
| 3 |
| 2x+12 |
考点:分式的加减法
专题:规律型
分析:(1)首先发现,分子都是1,分母是连续两个自然数的乘积,计算的结果就是以这两个自然数为分母,分子是1的两个分数的差;由此解决(1);再利用规律把(2)中的分数拆成两个分数的差,把互为相反数的互相抵消,得出答案即可.
(2)、(3)利用(1)中的规律进行解题.
(2)、(3)利用(1)中的规律进行解题.
解答:解:(1)∵
=1-
;
=
-
;
=
-
;
=
-
;…,
∴
=
-
.
故答案是:
-
.
(2)
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
;
(3)
+
+
=
,
-
+
-
+
-
=
,
-
=
,
2(x+6)-2x=3x,
3x=6,
x=2.
经检验x=2是原方程的解.
故原方程的解为:x=2.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
∴
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
故答案是:
| 1 |
| n |
| 1 |
| n+1 |
(2)
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
(3)
| 1 |
| x(x+2) |
| 1 |
| (x+2)(x+4) |
| 1 |
| (x+4)(x+6) |
| 3 |
| 2x+12 |
| 1 |
| x |
| 1 |
| x+2 |
| 1 |
| x+2 |
| 1 |
| x+4 |
| 1 |
| x+4 |
| 1 |
| x+6 |
| 3 |
| 2x+12 |
| 1 |
| x |
| 1 |
| x+6 |
| 3 |
| 2x+12 |
2(x+6)-2x=3x,
3x=6,
x=2.
经检验x=2是原方程的解.
故原方程的解为:x=2.
点评:此题考查数字的规律,发现数字之间的联系,找出规律,解决问题.

练习册系列答案
相关题目
函数y=2x-1的图象一定通过点( )
| A、(3,4) |
| B、(-2,3) |
| C、(2,7) |
| D、(1,1) |
下列各个单项式中,与2x4y是同类项的为( )
| A、-x4y |
| B、2xy |
| C、8xy4 |
| D、2x2y2 |
 如图,在⊙O中,弦AB的长为6cm,圆心O到AB的距离为4cm.求⊙O的半径.
如图,在⊙O中,弦AB的长为6cm,圆心O到AB的距离为4cm.求⊙O的半径.
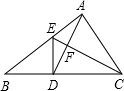 如图在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.BC=10,S△FCD=5.
如图在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.BC=10,S△FCD=5.