题目内容
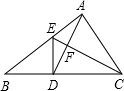 如图在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.BC=10,S△FCD=5.
如图在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.BC=10,S△FCD=5.(1)求证:△ABC∽△FCD;
(2)求S△ABC;
(3)求ED的长.
考点:相似三角形的判定与性质
专题:
分析:(1)证明∠B=∠ECD;证明∠ADC=∠ACD,即可解决问题.
(2)设△FDC、△ABC的面积分别为λ、μ.由△ABC∽△FCD,得到
=(
)2,结合BC=2DC,λ=5,求出μ即可解决问题.
(3)直接运用三角形的面积公式即可解决问题.
(2)设△FDC、△ABC的面积分别为λ、μ.由△ABC∽△FCD,得到
| λ |
| μ |
| DC |
| BC |
(3)直接运用三角形的面积公式即可解决问题.
解答: 解:(1)∵BD=CD,DE⊥BC,
解:(1)∵BD=CD,DE⊥BC,
∴BE=CE,∠B=∠ECD;
∵AD=AC,
∴∠ADC=∠ACD,
∴△ABC∽△FCD.
(2)设△FDC、△ABC的面积分别为λ、μ.
∵△ABC∽△FCD,
∴
=(
)2,而BC=2DC,λ=5,
∴μ=20,即S△ABC的值为20.
(3)∵μ=
BC•DE,而μ=20,BC=10,
∴DE=4.
 解:(1)∵BD=CD,DE⊥BC,
解:(1)∵BD=CD,DE⊥BC,∴BE=CE,∠B=∠ECD;
∵AD=AC,
∴∠ADC=∠ACD,
∴△ABC∽△FCD.
(2)设△FDC、△ABC的面积分别为λ、μ.
∵△ABC∽△FCD,
∴
| λ |
| μ |
| DC |
| BC |
∴μ=20,即S△ABC的值为20.
(3)∵μ=
| 1 |
| 2 |
∴DE=4.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深入观察探究命题图形结构特点,灵活选用有关定理来分析、推理或解答.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
关于x的一元二次方程x2-(2-x)x=3的二次项系数、一次项系数、常数项分别是( )
| A、1、-2、3 |
| B、2、-2、-3 |
| C、1、2、-3 |
| D、2、-2、3 |