题目内容
4. 钟楼是云南大学的标志性建筑之一,某校教学兴趣小组要测量钟楼的高度,如图,他们在点A处测得钟楼最高点C的仰角为45°,再往钟楼方向前进至点B处测得最高点C的仰角为54°,AB=7m,根据这个兴趣小组测得的数据,计算钟楼的高度CD.(tan36°≈0.73,结果保留整数).
钟楼是云南大学的标志性建筑之一,某校教学兴趣小组要测量钟楼的高度,如图,他们在点A处测得钟楼最高点C的仰角为45°,再往钟楼方向前进至点B处测得最高点C的仰角为54°,AB=7m,根据这个兴趣小组测得的数据,计算钟楼的高度CD.(tan36°≈0.73,结果保留整数).
分析 首先根据题意得:∠CAD=45°,∠CBD=54°,AB=7m,在Rt△ACD中,易求得BD=AD-AB=CD-7;在Rt△BCD中,可得BD=CD•tan36°,即可得CD•tan36°=CD-7,继而求得答案.
解答 解:根据题意得:∠CAD=45°,∠CBD=54°,AB=112m,
∵在Rt△ACD中,∠ACD=∠CAD=45°,
∴AD=CD,
∵AD=AB+BD,
∴BD=AD-AB=CD-7(m),
∵在Rt△BCD中,tan∠BCD=$\frac{BD}{CD}$,∠BCD=90°-∠CBD=36°,
∴tan36°=$\frac{BD}{CD}$,
∴BD=CD•tan36°,
∴CD•tan36°=CD-7,
∴CD=$\frac{7}{1-tan36°}$≈$\frac{7}{1-0.73}$≈26(m).
答:天塔的高度CD约为:26m.
点评 本题考查了仰角的知识.此题难度适中,注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
19.-$\sqrt{2}$的相反数是( )
| A. | $\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | -2 |
9.已知等腰三角形的一边长为8,另一边长为5,则它的周长为( )
| A. | 18 | B. | 21 | C. | 13或21 | D. | 18或21 |
 如图,在四边形ABCD中,已知AB∥CD,AB=CD,在不添加任何辅助线的前提下,要想该四边形成为菱形,只需再添加上的一个条件是AB=AD或AC⊥BD.
如图,在四边形ABCD中,已知AB∥CD,AB=CD,在不添加任何辅助线的前提下,要想该四边形成为菱形,只需再添加上的一个条件是AB=AD或AC⊥BD.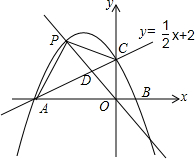 综合与探究:如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$,且经过A,C两点,与x轴的另一个交点为点B,正比例函数y=kx在第二象限与抛物线交于点P,与直线y=$\frac{1}{2}$x+2交于点D.
综合与探究:如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$,且经过A,C两点,与x轴的另一个交点为点B,正比例函数y=kx在第二象限与抛物线交于点P,与直线y=$\frac{1}{2}$x+2交于点D. 观察下列图形,它们是按一定规律排列的,依照此规律,第6个图形有38个太阳.
观察下列图形,它们是按一定规律排列的,依照此规律,第6个图形有38个太阳.