题目内容
13.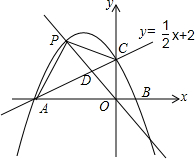 综合与探究:如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$,且经过A,C两点,与x轴的另一个交点为点B,正比例函数y=kx在第二象限与抛物线交于点P,与直线y=$\frac{1}{2}$x+2交于点D.
综合与探究:如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$,且经过A,C两点,与x轴的另一个交点为点B,正比例函数y=kx在第二象限与抛物线交于点P,与直线y=$\frac{1}{2}$x+2交于点D.(1)求抛物线的解析式;
(2)求△PAC面积的最大值,并求出此时点P的坐标;
(3)是否存在正比例函数y=kx,将△ABC的面积分为2:3的两部分?
分析 (1)由直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.可求得点A,与点C的坐标,然后利用对称性求得点B的坐标,再利用待定系数法求得函数的解析式;
(2)首先设P(m,-$\frac{1}{2}$m2-$\frac{3}{2}$m+2),过点P作PQ⊥x轴交AC于点Q,即可表示出PQ的长,继而表示出△PAC面积,则可求得答案;
(3)分别从当S△ADO:S四边形ODCB=2:3时与当S△ADO:S四边形ODCB=3:2时去分析求解即可求得答案.
解答 解:(1)∵对于直线y=$\frac{1}{2}$x+2,当x=0时,y=2;当y=0时,x=-4.
∴点C(0,2),A(-4,0).
∴由抛物线的对称性可知,点A与点B关于x=-$\frac{3}{2}$对称,
∴点B的坐标为B(1,0).
设抛物线的解析式为y=ax2+bx+c,可得
$\left\{\begin{array}{l}{c=2}\\{16a-4b+c=0}\\{a+b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-\frac{3}{2}}\\{c=2}\end{array}\right.$.
∴抛物线的解析式是y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2; (2)设P(m,-$\frac{1}{2}$m2-$\frac{3}{2}$m+2),
(2)设P(m,-$\frac{1}{2}$m2-$\frac{3}{2}$m+2),
如图1,过点P作PQ⊥x轴交AC于点Q.
∴Q(m,$\frac{1}{2}$m+2),
∴PQ=-$\frac{1}{2}$m2-$\frac{3}{2}$m+2-($\frac{1}{2}$m+2)=-$\frac{1}{2}$m2-2m,
∵S△APC=$\frac{1}{2}$×PQ×OA=$\frac{1}{2}$×PQ×4=2PQ,
∴S=2(-$\frac{1}{2}$m2-2m)=-m2-4m=-(m+2)2+4;
∴当m=-2时,△PAC的面积有最大值4.
此时P点坐标为(-2,3). (3)存在正比例函数y=kx,将△ABC的面积分为2:3的两部分.
(3)存在正比例函数y=kx,将△ABC的面积分为2:3的两部分.
则S△ABC=$\frac{1}{2}$×AB×OC=$\frac{1}{2}$×5×2=5,
分两种情况:
①如图2,过点D作DM1⊥AD,垂足为M1,
当S△ADO:S四边形ODCB=2:3时,S△ADO=$\frac{2}{5}$×5=2,
∴$\frac{1}{2}$×OA×DM1=2,即$\frac{1}{2}$×4×DM1=2,
∴DM1=1.
把y=1代入y=$\frac{1}{2}$x+2,得x=-2,
∴点D坐标为(-2,1).
把x=-2,y=1,代入正比例函数y=kx中,
解得:k=-$\frac{1}{2}$; ②如图3,过点D作DM2⊥AD,垂足为M2,
②如图3,过点D作DM2⊥AD,垂足为M2,
当S△ADO:S四边形ODCB=3:2时,S△ADO=$\frac{3}{5}$×5=3,
∴$\frac{1}{2}$×OA×DM2=3,即$\frac{1}{2}$×4×DM2=3,
∴DM2=$\frac{3}{2}$.
把y=$\frac{3}{2}$代入y=$\frac{1}{2}$x+2,得x=-1,
∴点D坐标为(-1,$\frac{3}{2}$).
把x=-1,y=$\frac{3}{2}$,代入正比例函数y=kx中,
解得:k=-$\frac{3}{2}$.
综上可得:k的值为-$\frac{1}{2}$或-$\frac{3}{2}$.
点评 此题属于二次函数的综合题,考查了待定系数求函数解析式的知识、三角形面积最值问题以及面积比问题.注意准确作出辅助线是解此题的关键.

| A. | (x2+3)(x2-3) | B. | (x2+3)(x+3)(x-3) | C. | (x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$) | D. | (x2+3)(x-$\sqrt{3}$) |
| A. | 23-24=2-1 | B. | (ab)2=a2b2 | C. | (a+b)2=a2+b2 | D. | a6÷a2=a3 |
| A. | m>1 | B. | m<1 | C. | m>4 | D. | m<4 |
 钟楼是云南大学的标志性建筑之一,某校教学兴趣小组要测量钟楼的高度,如图,他们在点A处测得钟楼最高点C的仰角为45°,再往钟楼方向前进至点B处测得最高点C的仰角为54°,AB=7m,根据这个兴趣小组测得的数据,计算钟楼的高度CD.(tan36°≈0.73,结果保留整数).
钟楼是云南大学的标志性建筑之一,某校教学兴趣小组要测量钟楼的高度,如图,他们在点A处测得钟楼最高点C的仰角为45°,再往钟楼方向前进至点B处测得最高点C的仰角为54°,AB=7m,根据这个兴趣小组测得的数据,计算钟楼的高度CD.(tan36°≈0.73,结果保留整数). 在矩形纸片ABCD中,AE=CG=$\sqrt{3}$,点P,Q分别是在边AB,CD上,BP=DQ,将△BGP和△DEQ分别沿PG,EQ翻折,点D,B的对应点分别是D′,B′,若四边形ED′GB′是有一边平行于AB的菱形(如图甲或图乙所示),且∠D′EB′=30°,则AP的长是2$\sqrt{3}$+1或3.
在矩形纸片ABCD中,AE=CG=$\sqrt{3}$,点P,Q分别是在边AB,CD上,BP=DQ,将△BGP和△DEQ分别沿PG,EQ翻折,点D,B的对应点分别是D′,B′,若四边形ED′GB′是有一边平行于AB的菱形(如图甲或图乙所示),且∠D′EB′=30°,则AP的长是2$\sqrt{3}$+1或3.