题目内容
7.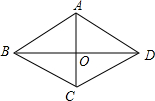 如图,在菱形ABCD中,点O是对角线的交点,|$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{DO}$|:|$\overrightarrow{CB}+\overrightarrow{CD}+\overrightarrow{AO}$|=$\sqrt{3}$,求菱形ABCD的内角度数.
如图,在菱形ABCD中,点O是对角线的交点,|$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{DO}$|:|$\overrightarrow{CB}+\overrightarrow{CD}+\overrightarrow{AO}$|=$\sqrt{3}$,求菱形ABCD的内角度数.
分析 根据菱形的对角线互相平分可得BO=DO,AO=CO,再根据向量的平行四边形法则表示出$\overrightarrow{BA}$+$\overrightarrow{BC}$,$\overrightarrow{CB}$+$\overrightarrow{CD}$,然后表示出|$\overrightarrow{BA}$+$\overrightarrow{BC}$+$\overrightarrow{DO}$|,|$\overrightarrow{CB}$+$\overrightarrow{CD}$+$\overrightarrow{AO}$|,从而求出$\frac{BO}{CO}$,再根据锐角三角函数的定义求出∠CBO,然后根据菱形的对角线平分一组对角求出∠ABC,再依次求解即可.
解答 解:在菱形ABCD中,BO=DO,AO=CO,
由向量的平行四边形法则得,$\overrightarrow{BA}$+$\overrightarrow{BC}$=$\overrightarrow{BD}$,$\overrightarrow{CB}$+$\overrightarrow{CD}$=$\overrightarrow{CA}$,
所以,|$\overrightarrow{BA}$+$\overrightarrow{BC}$+$\overrightarrow{DO}$|=|$\overrightarrow{BD}$+$\overrightarrow{DO}$|=|$\overrightarrow{BO}$|,
|$\overrightarrow{CB}$+$\overrightarrow{CD}$+$\overrightarrow{AO}$|=|$\overrightarrow{CA}$+$\overrightarrow{AO}$|=|$\overrightarrow{CO}$|,
∵|$\overrightarrow{BA}$+$\overrightarrow{BC}$+$\overrightarrow{DO}$|:|$\overrightarrow{CB}$+$\overrightarrow{CD}$+$\overrightarrow{AO}$|=$\sqrt{3}$,
∴$\frac{\overrightarrow{BO}}{\overrightarrow{CO}}$=$\sqrt{3}$,
∴$\frac{BO}{CO}$=$\sqrt{3}$,
又∵菱形ABCD对角线AC⊥BD,
∴∠CBO=30°,
∴∠ABC=2∠CBO=2×30°=60°,
∴∠BCD=180°-60°=120°,
∠ACD=∠ABC=60°,
∠BAD=∠BCD=120°.
点评 本题考查了平面向量,菱形的性质,向量的问题,熟练掌握平行四边形法则是解题的关键.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案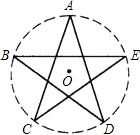 如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )
如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )| A. | a•sin72° | B. | $\frac{a}{tan72°}$ | C. | $\frac{a}{cos18°}$ | D. | $\frac{a}{cos36°}$ |
 如图所示的象棋盘上网格是由小正方形组成,若帅位于点(-2,-2)上,相位于点(2,-2)上,则炮位于点( )
如图所示的象棋盘上网格是由小正方形组成,若帅位于点(-2,-2)上,相位于点(2,-2)上,则炮位于点( )| A. | (-5,1) | B. | (-3,1) | C. | (-8,2) | D. | (-3,3) |
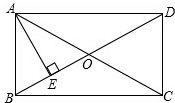 在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD,垂足为E,且AE平分∠BAO.若DO=2,求AB和BC的长度.
在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD,垂足为E,且AE平分∠BAO.若DO=2,求AB和BC的长度.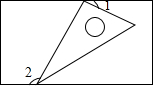 如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=125°.
如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=125°. 如图,已知∠1>∠2,如果把∠1沿着AD翻折过来,射线AB与∠2将会有怎样的位置关系?
如图,已知∠1>∠2,如果把∠1沿着AD翻折过来,射线AB与∠2将会有怎样的位置关系?