题目内容
9.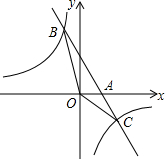 如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5)、C($\frac{5}{2}$,d)两点.
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5)、C($\frac{5}{2}$,d)两点.(1)求d,k,b的值;
(2)求SOBC.
分析 (1)将点B的坐标代入反比例函数解析式求得C的值,然后将x=$\frac{5}{2}$代入反比例函数的解析式求得d=-2,然后将点B、C的坐标代入一次函数的解析式求得k、b的值即可;
(2)先求得点A的坐标,然后用△AOB的面积+△COA的面积即可.
解答 解:(1)将(-1,5)代入y2=$\frac{c}{x}$得c=-5,
∴反比例函数得解析式为${y}_{2}=-\frac{5}{x}$.
将x=$\frac{5}{2}$代入反比例函数得解析式得:y2=-2,即d=-2,
将B(-1,5)、C($\frac{5}{2}$,-2)代入一次函数的解析式得;$\left\{\begin{array}{l}{-k+b=5}\\{\frac{5}{2}k+b=-2}\end{array}\right.$
解得:k=-2,b=7
(2)∵k=-2,b=7,
∴直线BC的解析式为y=-2x+7.
令y=0得:-2x+7=0,解得:x=$\frac{7}{2}$,
S△BOC=S△AOB+S△AOC
=$\frac{1}{2}×\frac{7}{2}×5+\frac{1}{2}×\frac{7}{2}×2$
=$\frac{49}{4}$.
点评 本题主要考查的是反比例函数和一次函数的交点,利用待定系数法求得函数的解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列不等式变形正确的是( )
| A. | 由4x-1≥0得4x>1 | B. | 由5x>3 得 x>3 | C. | 由$\frac{y}{2}$>0得 y>0 | D. | 由-2x<4得x<-2 |
20.在平面直角坐标系中,点(m-2,m-3)在第三象限,则m的取值范围是( )
| A. | m>3 | B. | m<2 | C. | 2<m<3 | D. | m<3 |
17.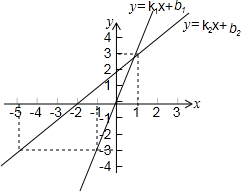 一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
 一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )| A. | x<-1 | B. | -5<x<1 | C. | -5<x<-1 | D. | -1<x<1 |
14.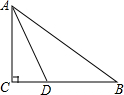 如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )
 如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )| A. | AC=6 | B. | AD=7 | C. | BC=8 | D. | AB=10 |
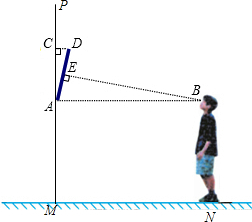 我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳,如图是小然站咋地面MN欣赏悬挂在墙壁PM上的油画AD(PM⊥MN)的示意图,设油画AD与墙壁的夹角∠PAD=α,此时小然的眼睛与油画底部A处于同一水平线上,视线恰好落在油画的中心位置E处,且与AD垂直.已知油画的高度AD为100cm.
我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳,如图是小然站咋地面MN欣赏悬挂在墙壁PM上的油画AD(PM⊥MN)的示意图,设油画AD与墙壁的夹角∠PAD=α,此时小然的眼睛与油画底部A处于同一水平线上,视线恰好落在油画的中心位置E处,且与AD垂直.已知油画的高度AD为100cm.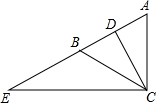 如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB到点E,使BE=AB,连接CE.求证:CD=$\frac{1}{2}$CE.
如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB到点E,使BE=AB,连接CE.求证:CD=$\frac{1}{2}$CE.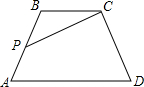 如图,已知AD∥BC,点P位AB上一点,设∠BCP=∠a,∠CPB=∠β.
如图,已知AD∥BC,点P位AB上一点,设∠BCP=∠a,∠CPB=∠β.