题目内容
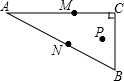 如图,在△ABC中,∠ACB=90°,∠A=30°,AC=
如图,在△ABC中,∠ACB=90°,∠A=30°,AC=| 3 |
考点:轴对称-最短路线问题
专题:
分析:设点P关于AC的对称点为K,关于AB的对称点为J,当点M、N在KJ上时,△PMN的周长最小.
解答: 解:分别作点P关于AC的对称点为K,关于AB的对称点为J,连接KJ,分别交AC、AB于点M、N,连接AP、AK、AJ、PM、PN.
解:分别作点P关于AC的对称点为K,关于AB的对称点为J,连接KJ,分别交AC、AB于点M、N,连接AP、AK、AJ、PM、PN.
∵点P关于AC的对称点为K,关于AB的对称点为J,
∴PM=KM,AP=AK,∠KAC=∠PAC;
∵点P关于AB的对称点为J,
∴PN=JN,AP=AJ,∠JAB=∠PAB,
∴AK=AJ=AP=1,∠KAJ=∠KAC+∠PAC+∠PAB+∠JAB=2∠PAC+2∠PAB=2∠BAC=60°,
∴△KAJ是等边三角形,
∴KJ=AK=AJ=1.
∴△PMN的周长的最小值=PM+MN+PN=KM+MN+JN≥KJ=1.
故答案为1.
 解:分别作点P关于AC的对称点为K,关于AB的对称点为J,连接KJ,分别交AC、AB于点M、N,连接AP、AK、AJ、PM、PN.
解:分别作点P关于AC的对称点为K,关于AB的对称点为J,连接KJ,分别交AC、AB于点M、N,连接AP、AK、AJ、PM、PN.∵点P关于AC的对称点为K,关于AB的对称点为J,
∴PM=KM,AP=AK,∠KAC=∠PAC;
∵点P关于AB的对称点为J,
∴PN=JN,AP=AJ,∠JAB=∠PAB,
∴AK=AJ=AP=1,∠KAJ=∠KAC+∠PAC+∠PAB+∠JAB=2∠PAC+2∠PAB=2∠BAC=60°,
∴△KAJ是等边三角形,
∴KJ=AK=AJ=1.
∴△PMN的周长的最小值=PM+MN+PN=KM+MN+JN≥KJ=1.
故答案为1.
点评:此题主要考查轴对称--最短路线问题以及等边三角形的性质,正确作出图形,理解△PMN周长最小的条件是解题的关键.

练习册系列答案
相关题目
下列函数中,图象经过点(
,-4)的反比例函数是( )
| 1 |
| 2 |
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
下列各组数是勾股数的是( )
| A、12、15、18 |
| B、0.3、0.4、0.5 |
| C、1.5、3、2.5 |
| D、12、16、20 |