题目内容
△ABC的高BD、CE所在的直线交于点H,若∠BHC=65°,则∠BAC的度数为 .
考点:多边形内角与外角
专题:
分析:分∠BAC是钝角,∠ABC是钝角,∠ACB是钝角,三种情况进行讨论,根据四边形内角和定理和同角的余角相等可求∠BAC的度数.
解答:解:如图1,∠BAC是钝角,

∠BAC=360°-90°×2-∠BHC=115°;
如图2,∠ABC是钝角,

根据同角的余角相等可得∠BAC=∠BHC=65°;
如图2,∠ACB是钝角,

根据同角的余角相等可得∠BAC=∠BHC=65°.
综上所述,∠BAC的度数为115°或65°.
故答案为:115°或65°.

∠BAC=360°-90°×2-∠BHC=115°;
如图2,∠ABC是钝角,

根据同角的余角相等可得∠BAC=∠BHC=65°;
如图2,∠ACB是钝角,

根据同角的余角相等可得∠BAC=∠BHC=65°.
综上所述,∠BAC的度数为115°或65°.
故答案为:115°或65°.
点评:考查了多边形内角与外角,本题关键是熟悉四边形内角和定理和余角的性质.注意分类思想的运用.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
18的算术平方根介于( )
| A、2到3之间 |
| B、3到4之间 |
| C、4到5之间 |
| D、5到6之间 |
 ABCD为一矩形纸片,AB=
ABCD为一矩形纸片,AB= 如图,在△ABC中,∠ACB=90°,∠A=30°,AC=
如图,在△ABC中,∠ACB=90°,∠A=30°,AC=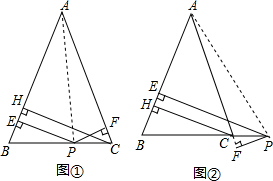
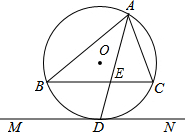 已知,△ABC内接于半径为5的⊙O,AD平分∠BAC,交直线BC于点E,交⊙O于点D.
已知,△ABC内接于半径为5的⊙O,AD平分∠BAC,交直线BC于点E,交⊙O于点D.