题目内容
在平面直角坐标系中作出y=-x2的图象,并根据图象回答下列问题:
(1)抛物线与x轴有交点吗?如果有,请写出交点坐标;
(2)指出此抛物线的对称轴及顶点坐标;
(3)当x<0时,随着x值的增大,y值如何变化?此时抛物线上这一部分图象的趋势可简称为什么?当x>0呢?
(4)当x=
时,y的值是多少?
(5)当y=-2时,x的值是多少?
(6)当x取何值时,y有最大值?最大值是多少?
(1)抛物线与x轴有交点吗?如果有,请写出交点坐标;
(2)指出此抛物线的对称轴及顶点坐标;
(3)当x<0时,随着x值的增大,y值如何变化?此时抛物线上这一部分图象的趋势可简称为什么?当x>0呢?
(4)当x=
| 1 |
| 2 |
(5)当y=-2时,x的值是多少?
(6)当x取何值时,y有最大值?最大值是多少?
考点:抛物线与x轴的交点,二次函数的图象,二次函数的性质
专题:
分析:利用抛物线的开口方向,顶点坐标,与坐标轴的交点坐标作出函数图象.
(1)、(2)、(3)、(6)根据抛物线可以直接写出答案.
(4)把x=
代入函数解析式即可求得相应的y的值;
(5)把y=-2代入函数解析式即可求得相应的x的值、
(1)、(2)、(3)、(6)根据抛物线可以直接写出答案.
(4)把x=
| 1 |
| 2 |
(5)把y=-2代入函数解析式即可求得相应的x的值、
解答: 解:y=-x2顶点坐标是(0,0),开口方向向下,对称轴是y轴.其图象如图所示.
解:y=-x2顶点坐标是(0,0),开口方向向下,对称轴是y轴.其图象如图所示.
(1)如图所示,抛物线与坐标轴交于原点,则与x轴没有交点;
(2)如图所示:抛物线的y=-x2顶点坐标是(0,0),对称轴是y轴;
(3)当x<0时,随着x值的增大,y的值增大;此时抛物线上这一部分图象的趋势可简称增函数.当x>0,y的值随着x的增大而减小,此时抛物线上这一部分图象的趋势可简称减函数;
(4)把x=
代入函数y=-x2得,y=-(
)2=-
.
(5)y=-2代入函数y=-x2得,-2=-(x)2,
解得 x=±
;
(6)如图,根据图示知,当x=0时,y取最大值,最大值是0.
 解:y=-x2顶点坐标是(0,0),开口方向向下,对称轴是y轴.其图象如图所示.
解:y=-x2顶点坐标是(0,0),开口方向向下,对称轴是y轴.其图象如图所示.(1)如图所示,抛物线与坐标轴交于原点,则与x轴没有交点;
(2)如图所示:抛物线的y=-x2顶点坐标是(0,0),对称轴是y轴;
(3)当x<0时,随着x值的增大,y的值增大;此时抛物线上这一部分图象的趋势可简称增函数.当x>0,y的值随着x的增大而减小,此时抛物线上这一部分图象的趋势可简称减函数;
(4)把x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(5)y=-2代入函数y=-x2得,-2=-(x)2,
解得 x=±
| 2 |
(6)如图,根据图示知,当x=0时,y取最大值,最大值是0.
点评:本题考查了抛物线与x轴的交点.解题时注意数形结合,降低解题的难度与梯度.

练习册系列答案
相关题目
18的算术平方根介于( )
| A、2到3之间 |
| B、3到4之间 |
| C、4到5之间 |
| D、5到6之间 |
若一个多边形的边数增加,它的外角和( )
| A、随着增加 | B、随着减小 |
| C、保持不变 | D、无法确定 |
下列说法正确的是( )
| A、+8的绝对值与-8的绝对值互为相反数 |
| B、数轴上原点两侧的两个点所对应的两个数的绝对值相等 |
| C、绝对值等于2的数是2 |
| D、既不是正数又不是负数的有理数的绝对值是0 |
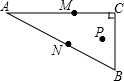 如图,在△ABC中,∠ACB=90°,∠A=30°,AC=
如图,在△ABC中,∠ACB=90°,∠A=30°,AC=