题目内容
12. 如图,B是线段AD上一动点,沿A→D→A以每秒2cm的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(t不超过10秒)
如图,B是线段AD上一动点,沿A→D→A以每秒2cm的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(t不超过10秒)(1)当t=2秒时,AB=4cm;
(2)当t=8秒时,求线段CD的长度;
(3)在运动过程中,若AB的中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.
分析 (1)根据速度乘以时间等于路程,可得答案;
(2)根据速度乘以时间等于路程,可得BD的长,根据线段中点的性质,可得答案;
(3)根据线段中点的性质,可得EB,BC的长,根据线段的和差,可得答案.
解答 解:(1)当t=2秒时,AB=2×2=4cm,
故答案为:4;
(2)当t=8秒时,BD=(8-5)×2=6cm,
CD=$\frac{1}{2}$BD=$\frac{1}{2}$×6=3cm,
线段CD的长度时3cm;
(3)不变,理由如下:
由AB的中点为E,C是线段BD的中点,得
EB=$\frac{1}{2}$AB,BC=$\frac{1}{2}$BD.
EC=$\frac{1}{2}$AB+$\frac{1}{2}$BD=$\frac{1}{2}$AD=$\frac{1}{2}$×10=5cm,
点评 本题考查了两点间的距离,利用线段中点的性质得出EB、BC的长是解题关键.

练习册系列答案
相关题目
2.下面解方程过程中变形正确的是( )
| A. | 方程4x+1=2x+1,移项,得4x+2x=0 | |
| B. | 方程,$\frac{x+1}{2}$=$\frac{3x-1}{2}$-1去分母,得x+1=3x-1-1 | |
| C. | 方程,$\frac{10}{7}$x-75+10x=10移项合并同类项,的$\frac{80}{7}$x=85 | |
| D. | 方程,$\frac{2x+1}{3}$-$\frac{x-1}{6}$=3去分母,得4x+2-x-1=18 |
1. 如图,阴影部分是一个长方形,它的面积是( )
如图,阴影部分是一个长方形,它的面积是( )
 如图,阴影部分是一个长方形,它的面积是( )
如图,阴影部分是一个长方形,它的面积是( )| A. | 3cm2 | B. | 4cm2 | C. | 5cm2 | D. | 6cm2 |
 正方形ABCD中,点E在边BC上,CE=2EB,连接AE、BD交于点F,∠DAE的角平分线交DC于点H,交BD于点M,将△MAD沿AD翻折得到△NAD,连接NF、NH、FH,若AB=3,则△NFH面积为$\frac{183}{8}$-6$\sqrt{10}$.
正方形ABCD中,点E在边BC上,CE=2EB,连接AE、BD交于点F,∠DAE的角平分线交DC于点H,交BD于点M,将△MAD沿AD翻折得到△NAD,连接NF、NH、FH,若AB=3,则△NFH面积为$\frac{183}{8}$-6$\sqrt{10}$. 如图中几何体由一些完全相同的小立方体组成,从上面看到图形的形状是( )
如图中几何体由一些完全相同的小立方体组成,从上面看到图形的形状是( )



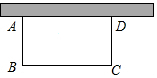 如图,用一段长为40m的篱笆围成一个一边靠墙的矩形花圃ABCD,墙长28m.设AB长为x m,矩形的面积为y m2.
如图,用一段长为40m的篱笆围成一个一边靠墙的矩形花圃ABCD,墙长28m.设AB长为x m,矩形的面积为y m2.