题目内容
18.已知|ab+2|+|a+1|=0,求下列式子的值:$\frac{1}{(a-b)(b+1)}+\frac{1}{(a-2)(b+2)}+…$+$\frac{1}{(a-2013)(b+2013)}$.
分析 利用绝对值求出a,b的值,再代入分式即可.
解答 解:∵|ab+2|+|a+1|=0,
∴ab+2=0,a+1=0,
解得a=-1,b=2,
∴原式=$\frac{1}{-2×3}$+$\frac{1}{-3×4}$+…+$\frac{1}{-2014×2015}$
=-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{3}$+$\frac{1}{4}$+…-$\frac{1}{2014}$+$\frac{1}{2015}$
=-$\frac{1}{2}$+$\frac{1}{2015}$
=-$\frac{2013}{4030}$.
点评 本题主要考查了分式化简,非负数的性质,解题的关键是求出a,b的值

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
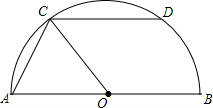 如图,AB是半圆O的直径,CD是半圆O的弦,CD∥AB,连接CO,AC,若∠BOC=124°,求∠ACD的度数.
如图,AB是半圆O的直径,CD是半圆O的弦,CD∥AB,连接CO,AC,若∠BOC=124°,求∠ACD的度数.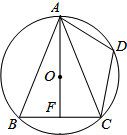 如图,⊙O是△ABC的外接圆,AO⊥BC于点F,D为$\widehat{AC}$的中点,且$\widehat{CD}$的度数为72°,求∠BAF的度数.
如图,⊙O是△ABC的外接圆,AO⊥BC于点F,D为$\widehat{AC}$的中点,且$\widehat{CD}$的度数为72°,求∠BAF的度数.