题目内容
2.先化简,再求值:(1)(a+1)(a-1)+a(1-a),其中a=2012;
(2)$\frac{{{x^2}-4x+4}}{{{x^2}-1}}÷(1-\frac{3}{x+1})$,然后选取一个合适的x代入求值.
分析 (1)先根据整式混合运算的法则把原式进行化简,再把a的值代入进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再选取合适的x的值代入进行计算即可.
解答 解:(1)原式=a2-1+a-a2
=a-1,
当a=2012时,原式=2011;
(2)原式=$\frac{(x-2)^{2}}{(x+1)(x-1)}$÷$\frac{x-2}{x+1}$
=$\frac{{(x-2)}^{2}}{(x+1)(x-1)}$•$\frac{x+1}{x-2}$
=$\frac{x-2}{x-1}$,
当x=3时,原式=$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
12.一个二次函数,当x=0时,y=-5,当x=-1时,y=-4,当x=2时,y=5,则这个二次函数的解析式是( )
| A. | y=2x2-x-5 | B. | y=2x2+x+5 | C. | y=2x2-x+5 | D. | y=2x2+x-5 |
10.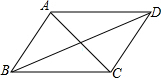 如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
 如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )| A. | 当AB=AD时,它是菱形 | B. | 当AC=BD时,它是矩形 | ||
| C. | 当AC⊥BD时,它是菱形 | D. | 当∠ABC=90°时,它是正方形 |
7.函数y=4x的图象不经过的点的坐标是( )
| A. | (0,0) | B. | (1,4) | C. | (1,-4) | D. | (-1,-4) |
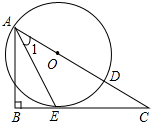 如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.