题目内容
17．
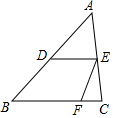如图，在△ABC中，D、E分别是AB、AC的中点，点F在BC上，DE是∠AEF的角平分线，若∠C=80°，则∠EFB的度数是（ ）| A． | 100° | B． | 110° | C． | 115° | D． | 120° |
分析 利用三角形中位线定理、平行线的性质、角平分线的性质以及邻补角的定义求得∠FEC，再由三角形内角和定理和邻补角的定义来求∠EFB的度数．
解答 解：∵在△ABC中，D、E分别是AB、AC的中点，
∴DE是中位线，
∴DE∥BC，
∴∠AED=∠C=80°．
又DE是∠AEF的角平分线，
∠DEF=∠AED=80°，
∴∠FEC=20°，
∴∠EFB=180°-∠C-∠FEC=100°．
故选：A．
点评 本题考查了三角形内角和定理，三角形中位线定理，根据三角形中位线性质得到DE与BC平行是解题的关键．
练习册系列答案
相关题目
5．
如图，在?ABCD中，∠ABC=60°，点E、F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，CF=$\sqrt{5}$．
（1）求证：四边形ABDE是平行四边形；
（2）连接DF，求DF的长．
如图，在?ABCD中，∠ABC=60°，点E、F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，CF=$\sqrt{5}$．（1）求证：四边形ABDE是平行四边形；
（2）连接DF，求DF的长．
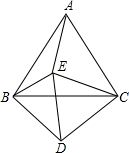如图，设△ABC和△CDE都是等边三角形，且∠EBD=62°，则∠AEB的度数是122°．
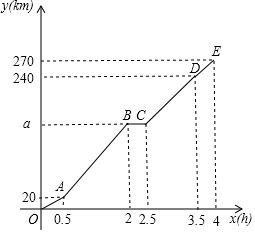小胜一家自驾去离家（点O）270km处的某景区（点E）旅游，如图折线OABCDE表示他们离家的路程y（km）与出发的时间x（h）之间的函数图象，其中AB段的行驶速度为90km/h，BC段表示小胜一家在高速服务区下车休息．
如图，矩形ABCD中，AB=2，点E在AD边上，以E为圆心EA长为半径的⊙E与BC相切，交CD于点F，连接EF．若扇形EAF的面积为$\frac{4}{3}$π，则BC的长是3．
7．某校食堂的中餐与晚餐的消费标准如表
一学生某星期从周一到周五每天的中餐与晚餐均在学校用餐，每次用餐米饭选1份，A、B类套餐菜选其中一份，这5天共消费36元，请问这位学生A、B类套餐菜各选用多少次？
| 种类 | 单价 |
| 米饭 | 0.5元/份 |
| A类套餐菜 | 3.5元/份 |
| B类套餐菜 | 2.5元/份 |