题目内容
2.在菱形ABCD中,一条边长为13,对角线AC=24,BD=10,则菱形的高是$\frac{120}{13}$.分析 先根据菱形的面积=两条对角线积的一半得出面积,再求出菱形的边长,由面积即可得出菱形的高.
解答 解:作DE⊥AB于E,如图所示: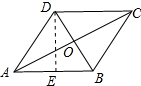 ∵四边形ABCD是菱形,对角线AC=24,BD=10,
∵四边形ABCD是菱形,对角线AC=24,BD=10,
∴AC⊥BD,OA=$\frac{1}{2}$AC=12,OB=$\frac{1}{2}$BD=5,
菱形ABCD的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×24×10=120,AB=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
又∵菱形ABCD的面积=AB•DE=120,
∴DE=$\frac{120}{13}$.
故答案为:$\frac{120}{13}$.
点评 本题考查了菱形的性质、勾股定理、菱形面积的计算;根据菱形的性质由勾股定理求出边长是解决问题的关键.

练习册系列答案
相关题目
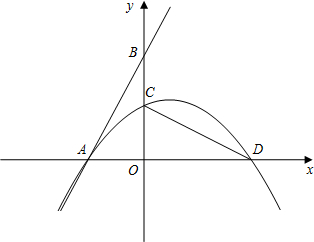 如图,在平面直角坐标系中,直线$y=-\frac{1}{2}{x^2}+\frac{1}{2}x+1$交Rt△COD轴于点A,交y轴于点B,将△AOB绕原点O顺时针旋转90°后得到△COD,抛物线经过点A、C、D.
如图,在平面直角坐标系中,直线$y=-\frac{1}{2}{x^2}+\frac{1}{2}x+1$交Rt△COD轴于点A,交y轴于点B,将△AOB绕原点O顺时针旋转90°后得到△COD,抛物线经过点A、C、D.