题目内容
某学生在解一元二次方程x（x-3）=x-3时，若他解得方程的解为x=1，则该同学丢掉的这个一元二次方程的解是 ．
考点：解一元二次方程-因式分解法
专题：计算题
分析：利用因式分解法求出已知方程的解，即可得到结果．
解答：解：x（x-3）=x-3，
整理得：x（x-3）-（x-3）=0，
分解因式得：（x-1）（x-3）=0，
可得x-1=0或x-3=0，
解得：x1=0，x2=3，
则丢掉的解为x=3，
故答案为：x=3
整理得：x（x-3）-（x-3）=0，
分解因式得：（x-1）（x-3）=0，
可得x-1=0或x-3=0，
解得：x1=0，x2=3，
则丢掉的解为x=3，
故答案为：x=3
点评：此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
天天练口算系列答案
相关题目
下列方程中是一元二次方程的是（ ）
| A、xy+2=1 | ||
| B、ax2+bx+c=0 | ||
| C、x2=0 | ||
D、x2+
|
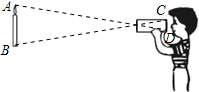如图，小强自制了一个小孔成像装置，其中纸筒的长度为15cm，他准备了一支长为20cm的蜡烛，想要得到高度为4cm的像，蜡烛与纸筒的距离应该为（ ）| A、60cm | B、65cm |
| C、70cm | D、75cm |
下列长度的四根木棒，能与3cm，7cm长的两根木棒钉成一个三角形的是（ ）
| A、3cm | B、4cm |
| C、6cm | D、10cm |
下列各数中，无理数是（ ）
| A、3.14 | ||
B、
| ||
C、
| ||
D、
|
一元二次方程（x+1）2=9可转化为两个一元一次方程，其中一个一元一次方程是x+1=3，则另一个一元二次方程是（ ）
| A、x-1=-3 |
| B、x-1=3 |
| C、x+1=3 |
| D、x+1=-3 |
如图，AD⊥AB，AD=AB，CE=CD，BE⊥BD，试判断线段CD和线段CE的位置关系，并证明．