题目内容
 如图,四边形ABCD是等腰梯形,BC∥AD,AB=DC,BD⊥CD,AC⊥AB,∠BAD=120°,AD=5,求等腰梯形ABCD的周长.
如图,四边形ABCD是等腰梯形,BC∥AD,AB=DC,BD⊥CD,AC⊥AB,∠BAD=120°,AD=5,求等腰梯形ABCD的周长.考点:等腰梯形的性质
专题:
分析:利用等腰梯形的性质结合锐角三角函数关系得出FC的长即可得出答案.
解答: 解:延长BC,使AD=CE,过点A作AM⊥BC于点M,过点D作DF⊥BC于点F,
解:延长BC,使AD=CE,过点A作AM⊥BC于点M,过点D作DF⊥BC于点F,
∵四边形ABCD是等腰梯形,BC∥AD,AB=DC,BD⊥CD,AC⊥AB,∠BAD=120°,
∴∠DAC=30°,BD=AC,∠BAD=∠ADC=120°,则∠CDF=30°,
∵AD
EC,
∴四边形ACED是平行四边形,
∴∠E=30°,
∴设FC=x,则DF=
x,
故tan30°=
=
=
,
解得:x=2.5,
故DC=AB=5,BC=BM+MF+FC=2.5+2.5+5=10,
则等腰梯形ABCD的周长为:5+5+5+10=25.
 解:延长BC,使AD=CE,过点A作AM⊥BC于点M,过点D作DF⊥BC于点F,
解:延长BC,使AD=CE,过点A作AM⊥BC于点M,过点D作DF⊥BC于点F,∵四边形ABCD是等腰梯形,BC∥AD,AB=DC,BD⊥CD,AC⊥AB,∠BAD=120°,
∴∠DAC=30°,BD=AC,∠BAD=∠ADC=120°,则∠CDF=30°,
∵AD
| ∥ |
. |
∴四边形ACED是平行四边形,
∴∠E=30°,
∴设FC=x,则DF=
| 3 |
故tan30°=
| DF |
| EF |
| ||
| x+5 |
| ||
| 3 |
解得:x=2.5,
故DC=AB=5,BC=BM+MF+FC=2.5+2.5+5=10,
则等腰梯形ABCD的周长为:5+5+5+10=25.
点评:此题主要考查了等腰梯形的性质以及锐角三角函数关系,得出FC的长是解题关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
点到直线的距离是指( )
| A、直线外一点到这条直线的垂线的长度 |
| B、直线外一点到这条直线上的任意一点的距离 |
| C、直线外一点到这条直线的垂线段 |
| D、直线外一点到这条直线的垂线段的长度 |
下列各选项中的两个直角三角形不一定全等的是( )
| A、两条直角边对应相等的两个直角三角形 |
| B、两个锐角对应相等的两个直角三角形 |
| C、斜边和一条直角边对应相等的两个直角三角形 |
| D、有一个锐角及这个锐角的对边对应相等的两个直角三角形全等 |
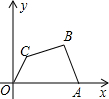 如图,在平面直角坐标系中,点A、B、C的坐标分别为A(5,0),B(4,3),C(1,2).
如图,在平面直角坐标系中,点A、B、C的坐标分别为A(5,0),B(4,3),C(1,2).