题目内容
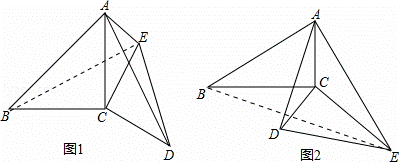
(1)如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
(2)如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.
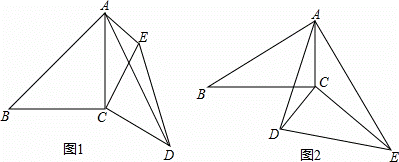
解:(1)如图1,连接BE,
∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,
又∵AC=BC,DC=EC,
在△ACD和△BCE中,
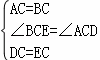 ,
,
∴△ACD≌△BCE,
∴AD=BE,
∵AC﹣BC=6,
∴AB=6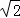 ,
,
∵∠BAC=∠CAE=45°
∴∠BAE=90°,
在Rt△BAE中,AB=6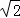 ,AE=3,
,AE=3,
∴BE=9,
∴AD=9;
(2)如图2,连接BE,
在Rt△ACB中,∠ABC=∠CED=30°,
tan30°=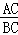 =
=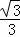 ,
,
∵∠ACB=∠DCE=90°,
∴∠BCE=∠ACD,
∴△ACD∽△BCE,
∴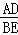 =
=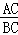 =
=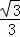 ,
,
∵∠BAC=60°,∠CAE=30°,
∴∠BAE=90°,又AB=6,AE=8,
∴BE=10,
∴AD=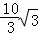 .
.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目

 )÷
)÷ ,其中x=
,其中x= .
.









 ,函数
,函数 的定义域为集合
的定义域为集合 ,则
,则
 B.
B. C.
C. D.
D.
 知函数
知函数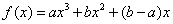 (a,b是不同时为零的常数),其导函数为
(a,b是不同时为零的常数),其导函数为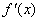 .
. 时,若不等式
时,若不等式 对任意
对任意
 恒成立,求b的取值范围;
恒成立,求b的取值范围;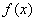 为奇函数,且在
为奇函数,且在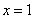 处的切线垂直于直线
处的切线垂直于直线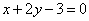 ,关于x的方程
,关于x的方程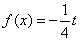 在
在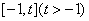 上有且只有一个实数根,求实数t的取值范围.
上有且只有一个实数根,求实数t的取值范围.