题目内容
4．
如图，扇形OAB中，∠AOB=60°，OA=6cm，则图中阴影部分的面积是（6π-9$\sqrt{3}$）cm2．
分析 根据S阴=S扇形OAB-S△AOB即可计算．
解答 解：∵OA=OB=6，∠AOB=60°，
∴△AOB是等边三角形，
∴S阴=S扇形OAB-S△AOB=$\frac{60π•{6}^{2}}{360}$-$\frac{\sqrt{3}}{4}$•62=（6π-9$\sqrt{3}$）cm2．
故答案为（6π-9$\sqrt{3}$）cm2．
点评 本题考查扇形面积公式、三角形面积公式，记住S扇形=$\frac{nπ{R}^{2}}{360}$=$\frac{1}{2}$LR（L是弧长，R是半径），等边三角形面积公式=$\frac{\sqrt{3}}{4}$a2，属于中考常考题型．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
14．下列各数中无理数是（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{22}{7}$ | C． | $\sqrt{4}$ | D． | $\root{3}{27}$ |
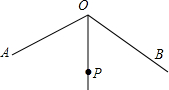如图，∠AOB=120°，OP平分∠AOB，且OP=2．若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有（ ）
已知直线l1：y=x+3与x轴交于点A，与y轴交于点B，且与双曲线y=$\frac{k}{x}$交于点C（1，a）．
如图，已知双曲线y=$\frac{k}{x}$与直线y=-x+6相交于A，B两点，过点A作x轴的垂线与过点B作y轴的垂线相交于点C，若△ABC的面积为8，则k的值为5．
9．一组数据2，x，4，3，3的平均数是3，则这组数据的中位数、众数、方差分别是（ ）
| A． | 3，3，0.4 | B． | 2，3，2 | C． | 3，2，0.4 | D． | 3，3，2 |
16．下面几何体中，其主视图与俯视图相同的是（ ）
| A． |  | B． |  | C． |  | D． |  |