Question

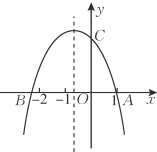
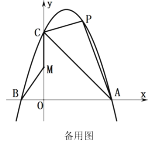
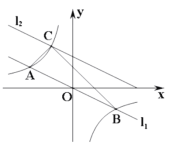
【题目】如图，在平面直角坐标系中，直线与反比例函数的图象交于A，B两点（点A在点B左侧），已知A点的纵坐标是1：将直线沿y向上平移后的直线与反比例函数在第二象限内交于点C，如果的面积为3，则平移后的直线的函数表达式为_____.

Answer 1

【答案】.

【解析】

先求出A点坐标，根据题意可得A、B关于原点对称，求出B点坐标. 设平移后的直线l2与y轴交于点D，连接AD和BD，可知△ABC的面积与△ABD的面积相等.由此可求出D点坐标. 直线的一次项系数与直线的一次项系数相同，它的常数项即为D点的纵坐标.

解：∵直线经过A点，且A点的纵坐标是1，

∴当y=1时，x=-2，

∴，

∵反比例函数与正比例函数都关于原点中心对称，

∴

如下图，设平移后的直线l2与y轴交于点D，连接AD和BD，

根据平移的性质，

∴△ABC的面积与△ABD的面积相等，

∵△ABC的面积为3，

，即，

∴，解得，

即平移后的直线的函数表达式为：.

故答案为：.