题目内容
【题目】已知△ABC为等边三角形, M为三角形外任意一点,把△ABM绕着点A按逆时针方向旋转60°到△CAN的位置.
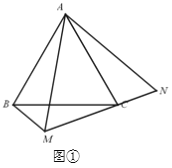
(1)如图①,若∠BMC=120°,BM=2,MC=3.求∠AMB的度数和求AM的长.
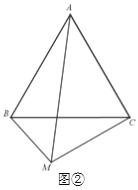
(2)如图②,若∠BMC = n°,试写出AM、BM、CM之间的数量关系,并证明你的猜想.
【答案】(1)60°,5;(2)AM=BM+CM
【解析】
(1)由旋转性质可得△ABM≌△CAN,根据全等三角形的性质和等边三角形的判定可得△AMN是等边三角形,继而求出∠AMN=60°,根据∠BMC=120°,∠AMN=∠AMC=60°,继而求出∠AMB;AM =MN= MC+ CN.
(2)
解∵把△ABM绕着点A按逆时针方向旋转60到△ACN的位置,
所以∠NAM=60°,
因为AN=AM,
所以△AMN是等边三角形,
所以∠AMN=60°,
因为∠BMC=120°,∠AMN=∠AMC=60°,
所以∠AMB=∠BMG-∠AMG=120°-60°=60°,
∵把△ABM绕着点A按逆时针方向旋转60°到△ACN的位置,
所以△ABM≌△CAN,
所以BM=CN=2,
△AMN是等边三角形
AM =MN= MC+ CN= 3+2=5,
故答案为60°,5;
(2)AM=BM+CM,
∵把△ABM绕着点A按逆时针方向旋转60°到△ACN的位置,
所以△ABM≌△CAN,
因为AN=AM,
所以△AMN是等边三角形,
所以∠AMN=60°,
因为∠BMC=n°,∠AMN=∠AMC=60°,
所以∠MNA=∠MAN,
所以MA=MN,
所以AM=BM+CM.

 名校课堂系列答案
名校课堂系列答案【题目】下表中给出了变量x与ax2,ax2+bx+c之间的部分对应值(表格中的符号“…”表示该项数据已经丢失)
x | -1 | 0 | 1 |
ax | … | … | 1 |
ax+ bx + c | 7 | 2 | … |
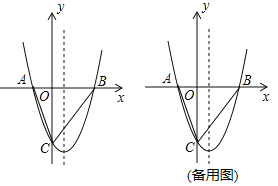
(1)写出这条抛物线的开口方向,顶点D的坐标;并说明它的变化情况;
(2)抛物线![]() 的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
(3)在(2)的条件下,设线段BD交x轴于点C,试写出∠BAD与∠DCO的数量关系,并说明理由.