题目内容
3. 已知△ABC中,∠ACD是外角,BE平分∠ABC,CE平分∠ACD,∠BEC=52°,求∠EAC的度数.
已知△ABC中,∠ACD是外角,BE平分∠ABC,CE平分∠ACD,∠BEC=52°,求∠EAC的度数.
分析 过点E作EF⊥BD于点F,作EG⊥AC于点G,作EH⊥BA于点H,求出∠CAH的度数,求出∠BAC,根据三角形的外角性质求出∠BAC=2∠BEC,即可求出答案.
解答 解:过点E作EF⊥BD于点F,作EG⊥AC于点G,作EH⊥BA于点H,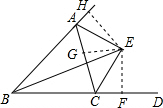
∵△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E,
∴EH=EF,EG=EF,
∴EH=EG,
∴AE是∠CAH的平分线,
∵∠BEC=52°,
∴∠BAC=2∠BEC,
∴∠BAC=104°,
∴∠CAH=76°,
∵BE平分∠ABC,CE平分∠ACD,
∴∠ACD=2∠ECD,∠ABC=2∠EBC,
∵∠ECD=∠BEC+∠EBC,∠ACD=∠ABC+∠BAC,
∴∠BEC=$\frac{1}{2}$∠BAC=52°,∠EAC=$\frac{1}{2}$∠CAH=38°.
点评 本题考查了三角形外角性质,角平分线性质的应用,主要考查学生运用性质进行推理的能力.

练习册系列答案
相关题目
14.某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.
(1)a=4,$\overline{{x}_{乙}}$=6;
(2)①分别计算甲、乙成绩的方差.
②请你从平均数和方差的角度分析,谁将被选中.
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲成绩 | 9 | 4 | 7 | 4 | 6 |
| 乙成绩 | 7 | 5 | 7 | a | 7 |
(2)①分别计算甲、乙成绩的方差.
②请你从平均数和方差的角度分析,谁将被选中.
 已知:如图,CB⊥AD,AE⊥DC,垂足分别B、E,AE、BC相交于点F,且AB=BC.求证:△ABF≌△CBD.
已知:如图,CB⊥AD,AE⊥DC,垂足分别B、E,AE、BC相交于点F,且AB=BC.求证:△ABF≌△CBD. 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,P是$\widehat{EF}$上的一点,若∠A=70°,求∠BOC、∠EPF的度数.
如图,⊙O是△ABC的内切圆,切点分别为D、E、F,P是$\widehat{EF}$上的一点,若∠A=70°,求∠BOC、∠EPF的度数.