题目内容
1.某餐厅中,一张桌子可坐6人,有以下两种摆放方式:(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待78位顾客共同就餐,但只有20张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?说明理由.
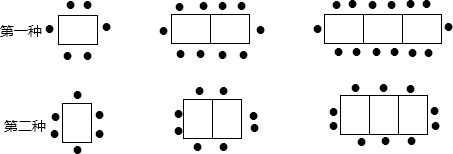
分析 (1)根据摆放规律,算出每种方式上下左右各能坐多少人,求和即可;
(2)由(1)中总结规律,让两种方式都等于78人,通过计算发现,第一种方式需要19张桌子,第二种方式需要37张桌子,而餐厅只有20张桌子,因此只能选择第一种方式.
解答 解:(1)方式一:当有n张桌子时
上方能坐2n个人,
下方能坐2n个人,
左右各有1人,共2人,
则方式一共能坐(4n+2)人;
方式二:当有n张桌子时
上方能坐n个人,
下方能坐n个人,
左右各有2人,共4人,
则方式二能坐(2n+4)人.
(2)选择第一种方式.
方式一:4n+2=78,n=19
方式二2n+4=78,n=37
∵餐厅只有20张餐桌,
∴选择方式一摆放.
点评 题目考查了图形的变化类,通过生活中实际例子,考查学生的观察能力和解决问题能力,题目整体难易程度适中,适合学生进行课后训练.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.⊙O的半径为3cm,如果圆心O到直线l的距离为d,且d=5cm,那么⊙O和直线l的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不确定 |
6.下列说法正确的是( )
| A. | 长度相等的弧叫等弧 | |
| B. | 平分弦的直径一定垂直于该弦 | |
| C. | 三角形的外心是三条角平分线的交点 | |
| D. | 不在同一直线上的三个点确定一个圆 |