题目内容
10.已知二次函数y=2x2-4x-6.(1)求抛物线的对称轴、顶点坐标.
(2)求图象与x轴的交点坐标,与y轴的交点坐标.
(3)当x为何值时,y随x的增大而增大?
(4)x为何值时y≥0?
分析 (1)将二次函数化为顶点式,即可得到抛物线的对称轴、顶点坐标;
(2)令y=0和x=0可以分别求得图象与x轴的交点坐标,与y轴的交点坐标;
(3)根据二次项系数和对称轴,可以得到当x为何值时,y随x的增大而增大;
(4)根据二次项系数和与x轴的交点,可以得到x为何值时y≥0.
解答 解:∵y=2x2-4x-6,
∴y=2(x-1)2-8,
∴该抛物线的对称轴为:直线x=1,顶点坐标是(1,-8),
当y=0时,0=2x2-4x-6,可得,x1=-1,x2=3,
当x=0时,y=-6,
∴图象与x轴的交点坐标是(-1,0)或(3,0),与y轴的交点坐标(0,-6),
∵a=2>0,对称轴为x=1,
∴当x>1时,y随x的增大而增大,
∴当x<-1或x>3时,y≥0,
由上可得,(1)抛物线的对称轴是直线x=1,顶点坐标是(1,-8);
(2)图象与x轴的交点坐标是(-1,0)或(3,0),与y轴的交点坐标是(0,-6);
(3)当>1时,y随x的增大而增大;
(4)当x<-1或x>3时,y≥0.
点评 本题考查二次函数的性质,解题的关键是明确二次函数的性质,能将二次函数解析式化为顶点式,明确与x轴相交时y=0,与y轴相交时x=0,由二次项系数可以和对称轴得到y随x如何变化,在什么范围内y≥0.

练习册系列答案
相关题目
20.下列四个点位于第三象限的是( )
| A. | (1,1) | B. | (4,-2) | C. | (-2,4) | D. | (-1,-2) |
2.整式-0.3x2y,0,$\frac{x+1}{2}$,$\frac{1}{a}$,$\frac{1}{3}$x2,-$\frac{1}{4}$y,-$\frac{1}{3}$ab2+$\frac{1}{2}$中,单项式的个数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
20. 已知如图所示的两个三角形全等,则∠α的度数是( )
已知如图所示的两个三角形全等,则∠α的度数是( )
 已知如图所示的两个三角形全等,则∠α的度数是( )
已知如图所示的两个三角形全等,则∠α的度数是( )| A. | 72° | B. | 60° | C. | 50° | D. | 58° |
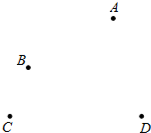 如图,平面上四个点A,B,C,D.按要求完成下列问题:
如图,平面上四个点A,B,C,D.按要求完成下列问题: