题目内容
12. 如图,已知AB=AC,BD=DC,AD的延长线交BC于点E.
如图,已知AB=AC,BD=DC,AD的延长线交BC于点E. (1)试说明BE=EC;
(2)试说明AD⊥BC.
分析 (1)根据SSS证明△ABD与△ACD全等,再利用等腰三角形的性质证明即可;
(2)根据等腰三角形的性质证明即可.
解答 证明:在△ABD与△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{BD=DC}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴△ABC是等腰三角形,
∴BE=EC;
(2)∵△ABC是等腰三角形,BE=EC,
∴AD⊥BC.
点评 此题考查全等三角形的判定和性质,以及等腰三角形的性质解答,关键是根据SSS证明△ABD与△ACD全等.

练习册系列答案
相关题目
20.下列各数是负数的是( )
| A. | 20 | B. | -5.21 | C. | $\frac{11}{7}$ | D. | 0 |
1.下列说法正确的是( )
| A. | 为了解全国中学生的心理健康情况,应该采用普查的方式 | |
| B. | 一个游戏的中奖概率是0.1,则做10次这样的游戏一定会中奖 | |
| C. | 为了调查中秋节期间市场上月饼质量情况,应该采用抽样调查的方式 | |
| D. | 若甲组数据的方差S甲2=0.01,乙组数据的方差S乙2=0.1,则乙组数据比甲级稳定 |
 如图,AB是⊙O的弦,∠B=30°,AB=2$\sqrt{3}$,m是过圆心O的一条直线,并绕点O做顺时针旋转运动,分别交圆于D、E两点.
如图,AB是⊙O的弦,∠B=30°,AB=2$\sqrt{3}$,m是过圆心O的一条直线,并绕点O做顺时针旋转运动,分别交圆于D、E两点.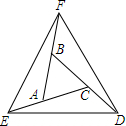 如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接点D、E、F,得到△DEF为等边三角形.
如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接点D、E、F,得到△DEF为等边三角形. 如图,从镜子中看到一钟表的时针和分针,此时的实际时刻是8:00.
如图,从镜子中看到一钟表的时针和分针,此时的实际时刻是8:00.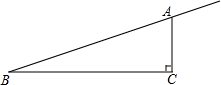 如图,在Rt△ABC中,∠ACB=90°,AC=1cm,BC=4cm,动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间,使得△PBC为等腰三角形.
如图,在Rt△ABC中,∠ACB=90°,AC=1cm,BC=4cm,动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间,使得△PBC为等腰三角形.