题目内容
1.观察下列等式:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,将以上三个等式两边分别相加得:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$.(1)计算:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2013×2014}$;
(2)参照上述解法计算:$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+$\frac{1}{7×9}$+…+$\frac{1}{2011×2013}$.
分析 (1)原式利用拆项法变形,计算即可得到结果;
(2)原式整理后,利用拆项法变形,计算即可得到结果.
解答 解:(1)原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2013}$-$\frac{1}{2014}$=1-$\frac{1}{2014}$=$\frac{2013}{2014}$;
(2)原式=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2011}$-$\frac{1}{2013}$)=$\frac{1}{2}$(1-$\frac{1}{2013}$)=$\frac{1006}{2013}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水目的,该市自来水收费价目表,如图所示,
(1)若该用户1月用水9m3,则应收水费24元;
(2)若该用户2月缴水费48元;求该用户2月用多少立方米的水?
(3)若该户居民3、4月份共用水15m3(4月份用水量超过3月份),共交水费44元,则该居民3、4各月份用水多少立方米?
| 价目表 | |
| 每月用水量 | 单价 |
| 不超出6m3的部分 | 2元/m3 |
| 超出6m3不超出10m3的部分 | 4元/m3 |
| 超出10m3的部分 | 8元/m3 |
| 注:消费按月结算 | |
(2)若该用户2月缴水费48元;求该用户2月用多少立方米的水?
(3)若该户居民3、4月份共用水15m3(4月份用水量超过3月份),共交水费44元,则该居民3、4各月份用水多少立方米?
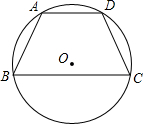 如图,四边形ABCD内接于⊙O,AD∥BC,求证:AB=CD.
如图,四边形ABCD内接于⊙O,AD∥BC,求证:AB=CD.