题目内容
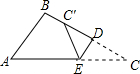如图，点D、E为△ABC边BC、AC上的两点，将△ABC沿线段DE折叠，点C落在BD上的C′处，若∠C=30°，则∠AEC′=________．
60°
分析：首先根据折叠可得EC=EC′，根据等边对等角可得∠EC′D=∠C，再根据三角形外角与内角的关系可得∠AEC′=∠C+∠C′，进而得到答案．
解答：根据折叠可得：EC=EC′，
∴∠EC′D=∠C，
∵∠C=30°，
∴∠EC′D=30°，
∴∠AEC′=30°+30°=60°，
故答案为：60°．
点评：此题主要考查了三角形内角与外角的关系，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．
分析：首先根据折叠可得EC=EC′，根据等边对等角可得∠EC′D=∠C，再根据三角形外角与内角的关系可得∠AEC′=∠C+∠C′，进而得到答案．
解答：根据折叠可得：EC=EC′，
∴∠EC′D=∠C，
∵∠C=30°，
∴∠EC′D=30°，
∴∠AEC′=30°+30°=60°，
故答案为：60°．
点评：此题主要考查了三角形内角与外角的关系，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
如图，点P的坐标为（2，
24、如图，点A的坐标为（2，-1），点B的坐标为（3，0），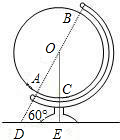
如图，点A、B为地球仪的南、北极点，直线AB与放置地球仪的平面交于点D，所成的角度约为60°，半径OC所在的直线与放置平面垂直，垂足为点E，DE=15cm，AD=14cm．
如图，点A在半径为3的⊙O内，OA=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
（2012•桂平市三模）如图，点P的坐标为（2，