题目内容
 如图,点P的坐标为(2,
如图,点P的坐标为(2,| 3 |
| 2 |
| k |
| x |
| k |
| x |
(1)求k的值.(2)求△APM的面积.
分析:(1)根据P的坐标为(2,
),PN=4先求出点N的坐标为(6,
),从而求出k=9.
(2)由k可求得反比例函数的解析式y=
.根据点M的横坐标求出其纵坐标y=
,得出MP=
-
=3,从而求得S△APM=
×2×3=3.
| 3 |
| 2 |
| 3 |
| 2 |
(2)由k可求得反比例函数的解析式y=
| 9 |
| x |
| 9 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵点P的坐标为(2,
),
∴AP=2,OA=
.
∵PN=4,∴AN=6,
∴点N的坐标为(6,
).
把N(6,
)代入y=
中,得k=9.
(2)∵k=9,∴y=
.
当x=2时,y=
.
∴MP=
-
=3.
∴S△APM=
×2×3=3.
| 3 |
| 2 |
∴AP=2,OA=
| 3 |
| 2 |
∵PN=4,∴AN=6,
∴点N的坐标为(6,
| 3 |
| 2 |
把N(6,
| 3 |
| 2 |
| k |
| x |
(2)∵k=9,∴y=
| 9 |
| x |
当x=2时,y=
| 9 |
| 2 |
∴MP=
| 9 |
| 2 |
| 3 |
| 2 |
∴S△APM=
| 1 |
| 2 |
点评:主要考查了待定系数法求反比例函数的解析式和反比例函数y=
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
| k |
| x |

练习册系列答案
相关题目
 (2012•桂平市三模)如图,点P的坐标为(2,
(2012•桂平市三模)如图,点P的坐标为(2, 已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧.
已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧. 如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 如图,点A的坐标为( )
如图,点A的坐标为( )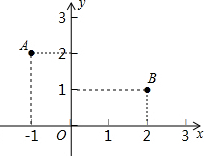 如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )
如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )