题目内容
7.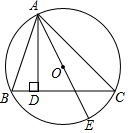 如图,AD为△ABC的高,AE为△ABC外接圆的直径,且AD=$\frac{1}{2}$AE=2$\sqrt{3}$,AB:AC=2:3,求sinB的值.
如图,AD为△ABC的高,AE为△ABC外接圆的直径,且AD=$\frac{1}{2}$AE=2$\sqrt{3}$,AB:AC=2:3,求sinB的值.
分析 连接CE,根据圆周角定理得到∠ACE=90°,设AB=2k,AC=3k,根据相似三角形的性质得到k=2,求得AB=4,然后根据三角函数的定义即可得到结论.
解答  解:连接CE,
解:连接CE,
∴∠B=∠E,
∵AE为△ABC外接圆的直径,
∴∠ACE=90°,
∵AD=$\frac{1}{2}$AE=2$\sqrt{3}$,
∴AE=4$\sqrt{3}$,
∵AB:AC=2:3,
∴设AB=2k,AC=3k,
∵AD为△ABC的高,
∴∠ADB=∠ACE=90°,
∴△ABD∽△AEC,
∴$\frac{AB}{AE}$=$\frac{AD}{AC}$,
∴$\frac{2k}{4\sqrt{3}}=\frac{2\sqrt{3}}{3k}$,
∴k=2,
∴AB=4,
∴sinB=$\frac{AD}{AB}$=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$.
点评 此题考查了相似三角形的判定和性质,圆周角定理与三角函数的定义.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想与转化思想的应用.

练习册系列答案
相关题目
2.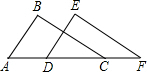 如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
 如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )| A. | ∠B=∠E | B. | ∠A=∠EDF | C. | ∠BCA=∠F | D. | BC∥EF |
12.用反证法证明“若a>b>0,则a2>b2”,应假设( )
| A. | a2<b2 | B. | a2=b2 | C. | a2≤b2 | D. | a2≥b2 |
15.若a:b=1:2,b:c=3:4,则a:b:c=( )
| A. | 1:6:4 | B. | 3:6:8 | C. | 1:6:8 | D. | 2:3:6 |
 求二次函数y=x2-4x+3的顶点坐标,并在所给坐标系中画出它的图象.
求二次函数y=x2-4x+3的顶点坐标,并在所给坐标系中画出它的图象.
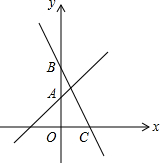 如图,已知函数y=x+2的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,4)且与x轴及y=x+2的图象分别交于点C、D,点D的坐标为($\frac{2}{3}$,n).
如图,已知函数y=x+2的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,4)且与x轴及y=x+2的图象分别交于点C、D,点D的坐标为($\frac{2}{3}$,n).