题目内容
阅读下列材料,并用相关的思想方法解决问题.
计算:(1﹣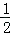 ﹣
﹣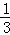 ﹣
﹣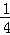 )×(
)×(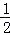 +
+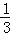 +
+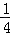 +
+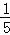 )﹣(1﹣
)﹣(1﹣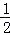 ﹣
﹣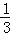 ﹣
﹣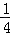 ﹣
﹣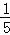 )×(
)×(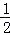 +
+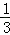 +
+ ).
).
令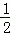 +
+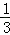 +
+ =t,则
=t,则
原式=(1﹣t)(t+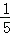 )﹣(1﹣t﹣
)﹣(1﹣t﹣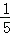 )t
)t
=t+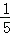 ﹣t2﹣
﹣t2﹣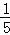 t﹣
t﹣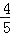 t+t2
t+t2
=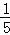
问题:
(1)计算
(1﹣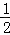 ﹣
﹣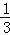 ﹣
﹣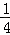 ﹣…﹣
﹣…﹣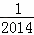 )×(
)×(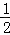 +
+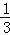 +
+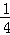 +
+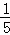 +…+
+…+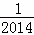 +
+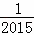 )﹣(1﹣
)﹣(1﹣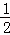 ﹣
﹣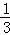 ﹣
﹣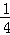 ﹣
﹣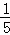 ﹣…﹣
﹣…﹣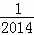 ﹣
﹣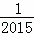 )×(
)×(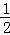 +
+ +
+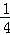 +…+
+…+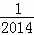 );
);
(2)解方程(x2+5x+1)(x2+5x+7)=7.
解:(1)设 +
+ +…+
+…+ =t,
=t,
则原式=(1﹣t)×(t+ )﹣(1﹣t﹣
)﹣(1﹣t﹣ )×t
)×t
=t+ ﹣t2﹣
﹣t2﹣ t﹣t+t2+
t﹣t+t2+ t
t
=0;
(2)设x2+5x+1=t,
则原方程化为:t(t+6)=7,
t2+6t﹣7=0,
解得:t=﹣7或1,
当t=1时,x2+5x+1=1,
x2+5x=0,
x(x+5)=0,
x=0,x+5=0,
x1=0,x2=﹣5;
当t=﹣7时,x2+5x+1=﹣7,
x2+5x+8=0,
b2﹣4ac=52﹣4×1×8<0,
此时方程无解;
即原方程的解为:x1=0,x2=﹣5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B.
B.  C.
C.  D.
D. 
 +
+ .
. 平均每亩产量为1.5x万千克,根据题意列方程为( )
平均每亩产量为1.5x万千克,根据题意列方程为( ) ﹣
﹣ =20 B.
=20 B.  ﹣
﹣ =20
=20 ﹣
﹣ +6sin60°+(π﹣3.14)0+|﹣
+6sin60°+(π﹣3.14)0+|﹣ |
| D.
D.  的解集是( )
的解集是( ) 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.
 .
.