题目内容
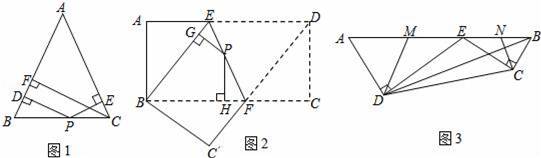
如图,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°.根据图形计算tan15°= .


2﹣
 .
.
【考点】解直角三角形.
【专题】几何综合题;压轴题.
【分析】此题可设AB=AC=2x,由已知可求出CD和AD,那么也能求出BD=AB﹣AD,从而求出tan15°.
【解答】解:由已知设AB=AC=2x,
∵∠A=30°,CD⊥AB,
∴CD=
 AC=x,
AC=x,
则AD2=AC2﹣CD2=(2x)2﹣x2=3x2,
∴AD=
 x,
x,
∴BD=AB﹣AD=2x﹣
 x=(2﹣
x=(2﹣
 )x,
)x,
∴tan15°=
 =
=
 =2﹣
=2﹣
 .
.
故答案为:2﹣
 .
.
【点评】此题考查的知识点是解直角三角形,关键是由直角三角形中30°角的性质与勾股定理先求出CD与AD,再求出BD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )3÷(
)3÷( )2
)2 2,其中a=
2,其中a= ,b=
,b= .
.




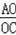
 的最小整数解是__________.
的最小整数解是__________.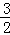 x+1,当自变量x取m时,对应的函数值大于0,设自变量分别取m﹣3,m+3时对应的函数值为y1,y2,则下列判断正确的是( )
x+1,当自变量x取m时,对应的函数值大于0,设自变量分别取m﹣3,m+3时对应的函数值为y1,y2,则下列判断正确的是( )