题目内容
阅读下面材料:
小明遇到下面一个问题:如图1所示,AD是△ABC的角平分线,AB=m,AC=n,求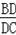
 的值.
的值.


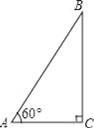
小明发现,分别过B,C作直线AD的垂线,垂足分别为E,F.通过推理计算,可以解决问题(如图2).请回答,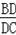
 = .
= .
参考小明思考问题的方法,解决问题:
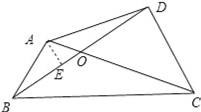
如图3,四边形ABCD中,AB=2,BC=6,∠ABC=60°,BD平分∠ABC,CD⊥BD.AC与BD相交于点O.
(1)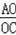
 = .
= .
(2)tan∠DCO= .
【考点】相似三角形的判定与性质.
【分析】小明的思路是先证明△BDF∽△CDE,得出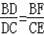
 ,再证明△ABF∽△ACE,得出
,再证明△ABF∽△ACE,得出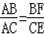
 ,因此得出
,因此得出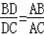
 .
.
(1)根据小明的结论得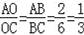
 ;
;
(2)作AE⊥BD于E,证明△AOE∽△COD,求出AE、BE、DE、OD、的长即可求出tan∠DCO的值.
【解答】解: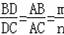
 ;
;
(1)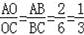
 ;
;
(2)作AE⊥BD于E,如图所示:
∵CD⊥BD,AE⊥BD,
∴AE∥CD,
∴△AOE∽△COD,
∴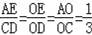
 ,
,
∵CD=3,∴AE=1,
∵BD平分∠ABC=60°,
∴∠ABD=∠DBC=30°,
∴BD=3
 ,
,
∵AB=2,
∴BE=
 ,
,
∴DE=2
 ,
,
∴OD=2
 ×
×
 =
=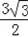
 ,
,
∴tan∠DCO=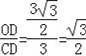
 .
.

【点评】本题考查了相似三角形的判定与性质以及锐角三角函数的运用;证明三角形相似是解决问题的关键.

练习册系列答案
相关题目






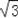

 都有意义的x的取值范围是__________.
都有意义的x的取值范围是__________.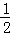 ,则锐角A的度数是( )
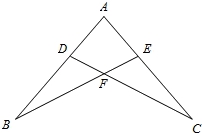
,则锐角A的度数是( )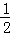 ,xn=
,xn= (n为不小于2的整数),则x2015= .
(n为不小于2的整数),则x2015= .