题目内容
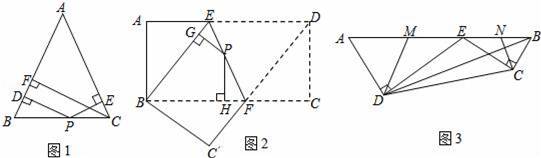
【问题情境】如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
【结论运用】如图2,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图3是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,
ED⊥AD,EC⊥CB,垂足分别为D、C,且AD•CE=DE•BC,AB=8,AD=3,BD=7;M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.

【考点】相似形综合题;等腰三角形的判定与性质;勾股定理;矩形的判定与性质.
【专题】压轴题;探究型.
【分析】【问题情境】连接AP,如图1,只需运用面积法(S△ABC=S△ABP+S△ACP)即可解决问题.
【结论运用】易证BE=BF,过点E作EQ⊥BF,垂足为Q,如图2,利用问题情境中的结论可得PG+PH=EQ,易证EQ=DC,BF=DF,只需求出BF即可.
【迁移拓展】如图3,由条件AD•CE=DE•BC联想到三角形相似,从而得到∠A=∠ABC,进而补全等腰三角形,△DEM与△CEN的周长之和就可转化为AB+BH,而BH是△ADB的边AD上的高,只需利用勾股定理建立方程,求出DH,再求出BH,就可解决问题.
【解答】【问题情境】证明:连接AP,如图1,
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP+S△ACP,
∴AB•CF=AB•PD+AC•PE.
∵AB=AC,∴CF=PD+PE;
【结论运用】解:过点E作EQ⊥BC,垂足为Q,如图2,
∵四边形ABCD是矩形,
∴AD=BC,∠C=∠ADC=90°.
∵AD=8,CF=3,
∴BF=BC﹣CF=AD﹣CF=5.
由折叠可得:DF=BF=5,∠BEF=∠DEF.
∵∠C=90°,∴DC=
 =
=
 =4.
=4.
∵EQ⊥BC,∠C=∠ADC=90°,
∴∠EQC=90°=∠C=∠ADC.
∴四边形EQCD是矩形,
∴EQ=DC=4.
∵AD∥BC,
∴∠DEF=∠EFB.
∵∠BEF=∠DEF,
∴∠BEF=∠EFB.
∴BE=BF.
由问题情境中的结论可得:PG+PH=EQ.
∴PG+PH=4.
即PG+PH的值为4;
【迁移拓展】解:延长AD、BC交于点F,作BH⊥AF,垂足为H,如图3.
∵ED⊥AD,EC⊥CB,
∴∠ADE=∠BCE=90°.
又∵AD•CE=DE•BC,即
 =
=
 ,
,
∴△ADE∽△BCE,
∴∠A=∠CBE,
∴FA=FB.
由问题情境中的结论可得:ED+EC=BH.
设DH=x,则AH=AD+DH=(3+x).
∵BH⊥AF,
∴∠BHA=90°.
∴BH2=BD2﹣DH2=AB2﹣AH2.
∵AB=8,AD=3,BD=7,
∴72﹣x2=82﹣(3+x)2.
解得:x=1.
∴BH2=BD2﹣DH2=49﹣1=48,
∴BH=4
 ,
,
∴ED+EC=BH=4
 .
.
∵∠ADE=∠BCE=90°,
且M、N分别为AE、BE的中点,
∴DM=AM=EM=AE,CN=BN=EN=BE.
∴△DEM与△CEN的周长之和
=DE+DM+EM+CN+EN+EC
=DE+AE+BE+EC=DE+AB+EC
=DE+EC+AB=8+4
 .
.
即△DEM与△CEN的周长之和为8+4
 .
.






【点评】本题考查了矩形的性质与判定、等腰三角形的性质与判定、全等三角形的性质与判定、相似三角形的性质与判定、平行线的性质与判定、直角三角形斜边上的中线等于斜边的一半、勾股定理等知识,考查了用面积法证明几何问题,考查了运用已有的经验解决问题的能力,体现了自主探究与合作交流的新理念,是充分体现新课程理念难得的好题.

 初中暑期衔接系列答案
初中暑期衔接系列答案.山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?
(2)该车行计划新进一批A型车和新款B型车共60辆,要使这批车获利不少于33000元,A型车至多进多少辆?A,B两种型号车的进货和销售价格如表:
|
| A型车 | B型车 |
| 进货价格(元) | 1100 | 1400 |
| 销售价格(元) | 今年的销售价格 | 2000 |
 ﹣
﹣ =
= ,ab=4,则a﹣b的值是__________.
,ab=4,则a﹣b的值是__________.
 x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=
x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=






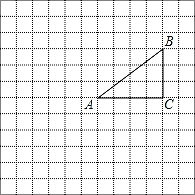
 C的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
C的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.