题目内容
已知二次函数y=﹣x2﹣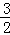 x+1,当自变量x取m时,对应的函数值大于0,设自变量分别取m﹣3,m+3时对应的函数值为y1,y2,则下列判断正确的是( )
x+1,当自变量x取m时,对应的函数值大于0,设自变量分别取m﹣3,m+3时对应的函数值为y1,y2,则下列判断正确的是( )
A.y1<0,y2<0 B.y1<0,y2>0 C.y1>0,y2<0 D.y1>0,y2>0
A【考点】二次函数图象上点的坐标特征.
【分析】求出二次函数与x轴的交点坐标,从而确定出m的取值范围,再根据二次函数图象上点的坐标特征解答即可.
【解答】解:令y=0,则﹣x2﹣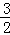 x+1=0,
x+1=0,
整理得,2x2+3x﹣2=0,
解得x 1
1 =﹣2,x2=
=﹣2,x2=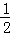 ,
,
所以,二次函数与x轴的交点坐标为(﹣2,0),(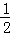 ,0),
,0),
所以,﹣2<m<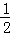 ,
,
∵m﹣3,m+3时对应的函数值为y1,y2,
∴y1<0,y2<0.
故选A.
【点评】本题考查了二次函数图象上点的坐标特征,抛物线与x轴的交点问题,求出函数图象与x轴的交点并确定出m的取值范围是解题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目


 ,则锐角A的度数是( )
,则锐角A的度数是( ) C的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
C的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.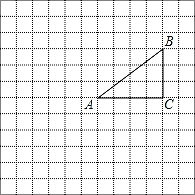
 ,那么x的值是( )
,那么x的值是( ) B.
B. C.
C. D.
D.
 (n为不小于2的整数),则x2015= .
(n为不小于2的整数),则x2015= .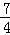 )2=
)2=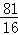 D.3x2﹣4x﹣2=0化为(x﹣
D.3x2﹣4x﹣2=0化为(x﹣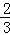 )2=
)2=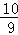
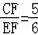
 ,CD=4,求BD的长.
,CD=4,求BD的长.
