题目内容
 如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( )
如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( )| A、30° | B、40° |
| C、45° | D、60° |
考点:等腰三角形的性质
专题:
分析:先根据等腰三角形的性质求出∠ADB的度数,再由平角的定义得出∠ADC的度数,根据等腰三角形的性质即可得出结论.
解答:解:∵△ABD中,AB=AD,∠B=80°,
∴∠B=∠ADB=80°,
∴∠ADC=180°-∠ADB=100°,
∵AD=CD,
∴∠C=
=
=40°.
故选:B.
∴∠B=∠ADB=80°,
∴∠ADC=180°-∠ADB=100°,
∵AD=CD,
∴∠C=
| 180°-∠ADC |
| 2 |
| 180°-100° |
| 2 |
故选:B.
点评:本题考查的是等腰三角形的性质,熟知等腰三角形的两底角相等是解答此题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
下列实数中是无理数的是( )
A、
| ||||
| B、2-2 | ||||
C、5.
| ||||
| D、sin45° |
 如图,以O为圆心的两个同心圆中,大圆与小圆的半径分别为3cm和1cm,若⊙P与这两个圆都相切,则圆P的半径为
如图,以O为圆心的两个同心圆中,大圆与小圆的半径分别为3cm和1cm,若⊙P与这两个圆都相切,则圆P的半径为 如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.过点B的直线y=-
如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.过点B的直线y=-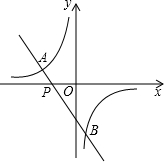 如图,一次函数y=kx+b(k≠0)的图象过点P(-
如图,一次函数y=kx+b(k≠0)的图象过点P(-