题目内容
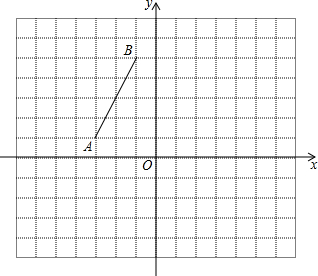 如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,线段AB的顶点均在格点上,且点A(-3,1)、B(-1,5).
如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,线段AB的顶点均在格点上,且点A(-3,1)、B(-1,5).(1)将线段AB沿一确定方向平移后得到线段A1B1,并且A1(2,-2),画出线段A1B1并直接写出B1的坐标;
(2)在方格纸中作出线段AB绕点O逆时针旋转90°后的对应线段A2B2;
(3)求出点A旋转到A2的过程中所经过的路程.
考点:作图-旋转变换,弧长的计算,作图-平移变换
专题:
分析:(1)根据平移变换的知识,可得线段AB向右平移5个单位,向下平移3个单位,作出线段A1B1并直接写出B1的坐标;
(2)分别作出点A和B绕点O逆时针旋转90°后的点,然后顺次连接;
(3)根据弧长公式求出点A旋转到A2的过程中所经过的路程.
(2)分别作出点A和B绕点O逆时针旋转90°后的点,然后顺次连接;
(3)根据弧长公式求出点A旋转到A2的过程中所经过的路程.
解答:解:(1)由题意得,线段AB平移后得到线段A1B1,需向右平移5个单位,向下平移3个单位,
所作图形如图所示:
B1的坐标为(4,2);
(2)所作图形如图所示;
(3)点A旋转到A2的过程中所经过的路程为圆心角为90°的弧长,
L=
=
.

所作图形如图所示:
B1的坐标为(4,2);
(2)所作图形如图所示;
(3)点A旋转到A2的过程中所经过的路程为圆心角为90°的弧长,
L=
90π×
| ||
| 180 |
| ||
| 2 |
点评:本题考查了根据旋转变换作图以及弧长公式,解答本题的关键是根据网格结构找出对应点的位置.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
下列方程中是一元二次方程的是( )
| A、5x2-6y-2=0 | ||
B、
| ||
| C、2x2-x-2=0 | ||
| D、ax2+bx+c=0 |
下列计算正确的是( )
| A、-[-(-ab2)2c]5=a10b20c5 | ||
| B、-(-3x2y3)3=-27x6y9 | ||
C、(
| ||
| D、(-0.3m3n2)3=-0.3m9n6 |
多项式a2+2ab+b2的次数是( )
| A、6 | B、4 | C、2 | D、以上的都不对 |
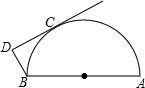 如图所示,已知AB是半圆O的直径,CD切半圆于C,BD⊥CD,若AB=2,∠DBA=140°,求BC的长.
如图所示,已知AB是半圆O的直径,CD切半圆于C,BD⊥CD,若AB=2,∠DBA=140°,求BC的长.