题目内容
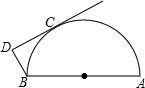 如图所示,已知AB是半圆O的直径,CD切半圆于C,BD⊥CD,若AB=2,∠DBA=140°,求BC的长.
如图所示,已知AB是半圆O的直径,CD切半圆于C,BD⊥CD,若AB=2,∠DBA=140°,求BC的长.考点:切线的性质
专题:
分析:连接OC,由切线的性质可得:OC∥DB,利用平行线的性质可求出∠COA的度数,进而可求出∠CAB的度数,利用∠CAB的正弦值即可求出BC的长.
解答:解:连接OC,
∵CD切半圆于C,
∴OC⊥DC,
∵BD⊥CD,
∴OC∥DB,
∴∠DBA=∠COA,
∵∠DBA=140°,
∴∠COA=140°,
∵OC=OA,
∴∠CAB=20°,
∵AB=2,
∴BC=2sin20°.
∵CD切半圆于C,
∴OC⊥DC,
∵BD⊥CD,

∴OC∥DB,
∴∠DBA=∠COA,
∵∠DBA=140°,
∴∠COA=140°,
∵OC=OA,
∴∠CAB=20°,
∵AB=2,
∴BC=2sin20°.
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
计算:
-
÷
的结果为( )
| x |
| x+3 |
| 6 |
| 9-x2 |
| 2 |
| x-3 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
下列计算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
一抛物线的图象向左平移2个单位,向上平移4个单位,得到的图象解析式为y=x2-4x+3,那么原抛物线的解析式是( )
| A、y=x2+3 | ||||
B、y=-
| ||||
C、y=-
| ||||
| D、y=x2-8x+11 |
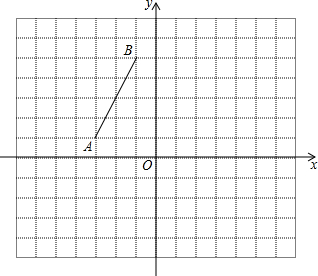 如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,线段AB的顶点均在格点上,且点A(-3,1)、B(-1,5).
如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,线段AB的顶点均在格点上,且点A(-3,1)、B(-1,5).