题目内容
在体育课上,老师用绳子围成了一个周长为36米的平行四边形ABCD游戏场地,其中∠ABC=45°,设AB的长为x米,平行四边形ABCD的面积为y平方米.
(1)求出y与x之间的函数关系式(直接写出自变量x的取值范围);
(2)求出x为何值时,平行四边形ABCD的面积最大,并求出最大值.
(1)求出y与x之间的函数关系式(直接写出自变量x的取值范围);
(2)求出x为何值时,平行四边形ABCD的面积最大,并求出最大值.
考点:二次函数的应用,平行四边形的性质
专题:
分析:(1)如图: 利用∠ABC=45°,设边AB的长为x,得出BC的长,进而表示出AE的长,进而得出平行四边形ABCD面积;
利用∠ABC=45°,设边AB的长为x,得出BC的长,进而表示出AE的长,进而得出平行四边形ABCD面积;
(2)利用公式法求出二次函数的最值即可.
 利用∠ABC=45°,设边AB的长为x,得出BC的长,进而表示出AE的长,进而得出平行四边形ABCD面积;
利用∠ABC=45°,设边AB的长为x,得出BC的长,进而表示出AE的长,进而得出平行四边形ABCD面积;(2)利用公式法求出二次函数的最值即可.
解答:解:(1)过点A作AE⊥BC于点E,
∵∠ABC=45°,
设边AB的长为x(单位:米),则BC=
(36-2x)m,
∴AE=ABsin45°=
xm,
∴平行四边形ABCD面积为:y=
x×
(36-2x),
即y=-
x2+9
x(0<x<18)
(2)∵a=-
<0,
∴抛物线开口向下,有最大值,
当x=-
=9时,
y的最大值为=
=
,
所以当x=9时,面积最大,最大值为
.
∵∠ABC=45°,
设边AB的长为x(单位:米),则BC=
| 1 |
| 2 |
∴AE=ABsin45°=
| ||
| 2 |
∴平行四边形ABCD面积为:y=
| ||
| 2 |
| 1 |
| 2 |
即y=-
| ||
| 2 |
| 2 |
(2)∵a=-
| ||
| 2 |
∴抛物线开口向下,有最大值,
当x=-
9
| ||||
-
|
y的最大值为=
-(9
| ||||
4×(-
|
81
| ||
| 2 |
所以当x=9时,面积最大,最大值为
81
| ||
| 2 |
点评:此题主要考查了平行四边形的性质以及二次函数最值求法,注意表示出平行四边形的高求出解析式是解题关键.

练习册系列答案
相关题目
一个多边形的每个内角都是144°,这个多边形是( )
| A、八边形 | B、十边形 |
| C、十二边形 | D、十四边形 |
 如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32cm,求△BCD的面积.
如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32cm,求△BCD的面积.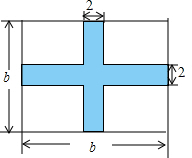 如图,在一块长为a米,宽为b米的长方形草地上,修建两条宽为2米的甬道.
如图,在一块长为a米,宽为b米的长方形草地上,修建两条宽为2米的甬道.