题目内容
13．
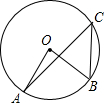如图，点A、B、C都在⊙O上，若∠AOB=76°，则∠ACB的度数为（ ）| A． | 19° | B． | 30° | C． | 38° | D． | 76° |
分析 由⊙O是△ABC的外接圆，∠AOB=76°，利用在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠ACB的度数．
解答 解：∵⊙O是△ABC的外接圆，∠AOB=76°，
∴∠ACB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×76°=38°．
故选C．
点评 此题考查了圆周角定理．此题比较简单，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用．
练习册系列答案
相关题目
4．
如图，用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5，弧长是6π，那么围成的圆锥的高度是（ ）
如图，用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5，弧长是6π，那么围成的圆锥的高度是（ ）| A． | $\sqrt{11}$ | B． | 5 | C． | 4 | D． | 3 |
1．比-2小的数是（ ）
| A． | -4 | B． | $\frac{1}{2}$ | C． | 0 | D． | -1 |
8．
如图，在?ABCD中若BE：EC=4：5，则BF：FD=（ ）
如图，在?ABCD中若BE：EC=4：5，则BF：FD=（ ）| A． | 4：5 | B． | 4：10 | C． | 4：9 | D． | 5：9 |
18．下列各式中，正确的是（ ）
| A． | -（2x+5）=2x+5 | B． | -$\frac{1}{2}$（4x-2）=-2x+2 | C． | -a+b=-（a-b） | D． | 2-3x=（3x+2） |
5．
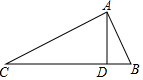如图所示，△ABC中，∠BAC=90°，AD⊥BC于D，若AB=3，BC=5，则DC的长度（ ）
如图所示，△ABC中，∠BAC=90°，AD⊥BC于D，若AB=3，BC=5，则DC的长度（ ）| A． | $\frac{16}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{8}{5}$ | D． | $\frac{22}{5}$ |
2．
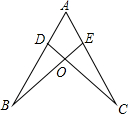如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（ ）
如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（ ）| A． | ∠B=∠C | B． | BE=CD | C． | BD=CE | D． | AD=AE |
