题目内容
13．
如图，在△ABC中，∠C=90°，AD平分∠CAB；DE⊥AB于E，若AC=8，则AE=8．
分析 根据角平分线上的点到角的两边距离相等可得CD=DE，然后利用“HL”证明Rt△ACD和Rt△AED全等，根据全等三角形对应边相等可得AE=AC．
解答 解：∵∠C=90°，AD平分∠CAB；DE⊥AB于E，
∴CD=DE，
在Rt△ACD和Rt△AED中，
$\left\{\begin{array}{l}{AD=AD}\\{CD=DE}\end{array}\right.$，
∴Rt△ACD≌Rt△AED（HL），
∴AE=AC=8．
故答案为：8．
点评 本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，熟记性质并确定出全等三角形是解题的关键．
练习册系列答案
相关题目
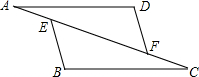如图，已知：AD∥BC，AD=CB，AE=CF．求证：∠D=∠B．
如图：AB∥CD，∠B=∠D，求证：AD∥BC．
如图，⊙O是△ABC的外接圆，若∠ACO=30°，则∠B的度数为60°．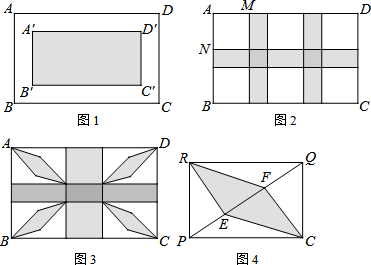
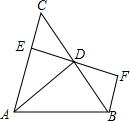如图，AD是△ABC的高，BF∥AC，过D点的直线交AC于点E，交BF于点F，DE=DF．
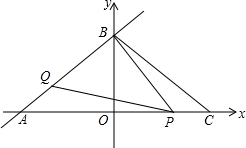如图，直线l：y=$\frac{3}{4}x+$3交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．