题目内容
18.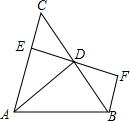 如图,AD是△ABC的高,BF∥AC,过D点的直线交AC于点E,交BF于点F,DE=DF.
如图,AD是△ABC的高,BF∥AC,过D点的直线交AC于点E,交BF于点F,DE=DF.求证:
(1)AB=AC;
(2)BC平分∠ABF.
分析 (1)先利用已知条件证明△CDE≌△BDF,得到CD=BD,由AD是△ABC的高,所以AD垂直平分线段BC,利用垂直平分线的性质得到AC=AB.
(2)由AB=AC,根据等边对等角,得∠C=∠ABC,又∠C=∠DBF,所以∠ABC=∠DBF,即BC平分∠ABF.
解答 解:(1)∵BF∥AC,
∴∠C=∠DBF,
在△CDE和△BDF中,
$\left\{\begin{array}{l}{∠C=∠DBF}\\{∠CDE=∠BDF}\\{DE=DF}\end{array}\right.$
∴△CDE≌△BDF,
∴CD=BD,
∵AD是△ABC的高,
∴AD垂直平分线段BC,
∴AC=AB.
(2)∵AB=AC,
∴∠C=∠ABC,
∵∠C=∠DBF,
∴∠ABC=∠DBF,
∴BC平分∠ABF.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明△CDE≌△BDF.

练习册系列答案
相关题目
8.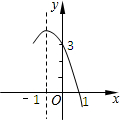 抛物线y=-x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是( )
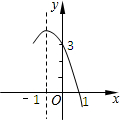 抛物线y=-x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是( )| A. | -4<x<1 | B. | x<-3或x>1 | C. | x<-4或x>1 | D. | -3<x<1 |
10.已知6m5nx÷2myn3=3m2n2,则( )
| A. | x=3,y=2 | B. | x=5,y=3 | C. | x=3,y=5 | D. | x=2,y=3 |
7.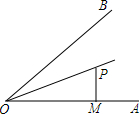 如图,若∠AOB的平分线上一点P到OA的距离PM等于5,N是射线OB上的任一点,则关于PN的长( )
如图,若∠AOB的平分线上一点P到OA的距离PM等于5,N是射线OB上的任一点,则关于PN的长( )
 如图,若∠AOB的平分线上一点P到OA的距离PM等于5,N是射线OB上的任一点,则关于PN的长( )
如图,若∠AOB的平分线上一点P到OA的距离PM等于5,N是射线OB上的任一点,则关于PN的长( )| A. | PN>5cm | B. | PN<5cm | C. | PN≥5cm | D. | PN≤5cm |
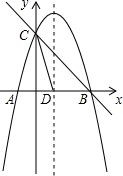 如图,抛物线y=-x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,3).
如图,抛物线y=-x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,3).
 如图,在△ABC中,∠C=90°,AD平分∠CAB;DE⊥AB于E,若AC=8,则AE=8.
如图,在△ABC中,∠C=90°,AD平分∠CAB;DE⊥AB于E,若AC=8,则AE=8.