题目内容
12.已知a,b,c是△ABC的三边,且a2+b2+c2=ab+ac+bc,求证:△ABC是等边三角形.分析 根据a2+b2+c2=ab+ac+bc,通过变形可得a、b、c之间的关系,从而可以证得结论成立.
解答 证明:∵a2+b2+c2=ab+ac+bc,
∴2a2+2b2+2c2=2ab+2ac+2bc
即(a2-2ab+b2)+(a2-2ac+c2)+(b2-2bc+c2)=0
得,(a-b)2+(a-c)2+(b-c)2=0
∴a-b=0,a-c=0,b-c=0
得a=b,a=c,b=c
∴a=b=c
∵a,b,c是△ABC的三边,
∴△ABC是等边三角形.
点评 本题考查等边三角形的性质、因式分解,解题的关键是可以将题目中的式子变为几个式子平方和的式子.

练习册系列答案
相关题目
1.半径为3的圆,如果半径增加2x,则面积S与x之间的函数表达式为( )
| A. | S=2π(x+3)2 | B. | S=9π+x | C. | S=4πx2+12x+9 | D. | S=4πx2+12πx+9π |
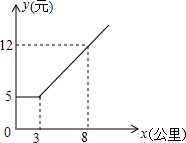 某市出租车公司收费标准如图所示,x(公里)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:
某市出租车公司收费标准如图所示,x(公里)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题: