Question

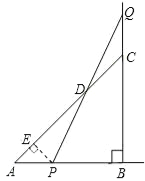
【题目】如图，P是边长为3的等边△ABC边AB上一动点，沿过点P的直线折叠∠B，使点B落在AC上，对应点为D，折痕交BC于E，点D是AC的一个三等分点，PB的长为______.

Answer 1

【答案】或

【解析】

两种情形：①如图1中，当AD＝AC＝1时，设PB＝x，②如图2中，当AD＝AC＝2时，利用相似三角形的性质求解即可．

解：两种情形：①如图1中，当AD＝AC＝1时，设PB＝x，

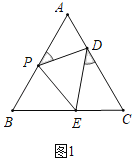
∵△ABC是等边三角形，

∴AB＝BC＝AC＝3，∠A＝∠B＝∠C＝60°，

∵∠PDE＝∠B＝60°，∠PDC＝∠PDE+∠EDC＝∠A+∠APD，

∴60°+∠EDC＝60°+∠APD，

∴∠EDC＝∠APD，

∴△APD∽△CDE，

∴，

∴，

∴BE＝DE＝，EC＝，

∵BE+EC＝3，

∴+＝3，

∴x＝．

②如图2中，当AD＝AC＝2时，

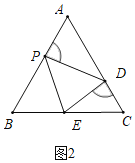
由△APD∽△CDE，可得，

∴，

∴DE＝，EC＝，

∵BE+EC＝3，

∴＝3，

∴x＝，

综上所述，PB的长为或．