题目内容
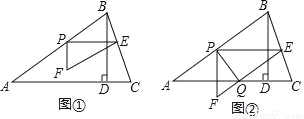
如图①,在锐角△ABC中,AB=5,tanC=3,BD⊥AC于点D,BD=3,点P从点A出发,以每秒1个单位长度的速度沿AB向终点B运动,过点P作PE∥AC交边BC于点E,以PE为边作Rt△PEF,使∠EPF=90°,点F在点P的下方,且EF∥AB.设△PEF与△ABD重叠部分图形的面积为S(平方单位)(S>0),点P的运动时间为t(秒)(t>0).
(1)求线段AC的长.
(2)当△PEF与△ABD重叠部分图形为四边形时,求S与t之间的函数关系式.
(3)若边EF与边AC交于点Q,连结PQ,如图②.
①当PQ将△PEF的面积分成1:2两部分时,求AP的长.
②直接写出PQ的垂直平分线经过△ABC的顶点时t的值.
练习册系列答案
相关题目

 B.
B.  C.
C.  D.
D. 
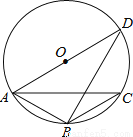
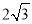 C. 3
C. 3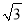 D. 2
D. 2